
分析 根据函数的凹凸性的定义,函数的单调性判断①②④,举例判断③.
解答 解:①因为在区间(a,b)上,f''(x)<0恒成立,
所以f'(x)在区间(a,b)单调减,所以结论成立,故①正确;
②f(x)=lnx,f'(x)=$\frac{1}{x}$,f″(x)=-$\frac{1}{{x}^{2}}$<0恒成立,
故在任意正实数区间(a,b)上都是凸函数,故②正确;
③举反例说明:如:函数f(x)=-x2,g(x)=-$\frac{1}{x}$在区间(0,1)都是凸函数,
但是f(x)•g(x)=x在区间(0,1)不是凸函数,③错误;
④若在区间(a,b)上f″(x)<0恒成立,函数f(x)在(a,b)上为“凸函数“.
在其图象上任意一点(x,f(x))处的切线的斜率随x的增大而减小,
根据图象可知对任意x1,x2∈(a,b)(x1≠x2)都有f($\frac{{x}_{1}+{x}_{2}}{2}$)>$\frac{f({x}_{1})+f({x}_{2})}{2}$,故④正确.
故答案为:①②④.
点评 本题考查了函数的单调性,导数的应用,“凸函数”的定义.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-1,1] | C. | [1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学平均名次 物理平均名次 | 1.3 2.3 | 12.3 9.7 | 25.7 31.0 | 36.7 22.3 | 50.3 40.0 | 67.7 58.0 | 49.0 39.0 | 52.0 60.7 | 40.0 63.3 | 34.3 42.7 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学平均名次 物理平均名次 | 78.3 49.7 | 50.0 46.7 | 65.7 83.3 | 66.3 59.7 | 68.0 50.0 | 95.0 101.3 | 90.7 76.7 | 87.7 86.0 | 103.7 99.7 | 86.7 99.0 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
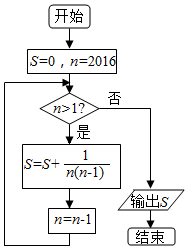
| A. | $\frac{1}{2016}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{1}{2015}$ | D. | $\frac{2014}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com