
一个半径为1的小球在一个内壁棱长为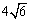 的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是
的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是
 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
现有4名教师参加说课比赛,共有4道备选题目,若每位教师从中有放回地随机选出一道题目进行说课,其中恰有一道题目没有被这4位教师选中的情况有( )
A.288种 B.144种 C.72种 D.36种
查看答案和解析>>
科目:高中数学 来源: 题型:
将平面向量的数量积运算与实数的乘法运算相类比,易得下列结论:
(1)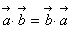
(2)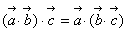
(3)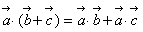
(4)由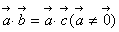 可得
可得
以上通过类比得到的结论正确的有:( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
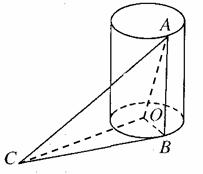
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线。
(1)求证:OB⊥AC;
(2)若AC与圆柱下底面所成的角为30°,OA=2。求三棱锥A-BOC的体积。
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数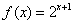 定义在R上.
定义在R上.
(1)若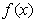 可以表示为一个偶函数
可以表示为一个偶函数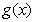 与一个奇函数
与一个奇函数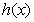 之和,设
之和,设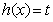 ,
,
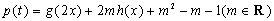 ,求出
,求出 的解析式;
的解析式;
(2)若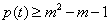 对于
对于 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(3)若方程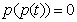 无实根,求m的取值范围.
无实根,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com