
【题目】一袋中有大小相同的4个红球和2个白球,给出下列结论:①从中任取3球,恰有一个白球的概率是![]() ;②从中有放回的取球6次,每次任取一球,恰好有两次白球的概率为
;②从中有放回的取球6次,每次任取一球,恰好有两次白球的概率为![]() ;③现从中不放回的取球2次,每次任取1球,则在第一次取到红球后,第二次再次取到红球的概率为
;③现从中不放回的取球2次,每次任取1球,则在第一次取到红球后,第二次再次取到红球的概率为![]() ;④从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为
;④从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为![]() . 则其中正确命题的序号是( )
. 则其中正确命题的序号是( )
A.①B.②C.③D.④
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,动点P,Q从点
中,动点P,Q从点![]() 出发在单位圆上运动,点P按逆时针方向每秒钟转
出发在单位圆上运动,点P按逆时针方向每秒钟转![]() 弧度,点Q按顺时针方向每秒钟转
弧度,点Q按顺时针方向每秒钟转![]() 弧度,则P,Q两点在第2019次相遇时,点P的坐标为________.
弧度,则P,Q两点在第2019次相遇时,点P的坐标为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前n项和为Sn,若S3=15,且a3+1为a1+1和a7+1的等比中项.
(1)求数列{an}的通项公式与前n项和Sn;
(2)设Tn为数列{![]() }的前n项和,问是否存在常数m,使Tn=m[
}的前n项和,问是否存在常数m,使Tn=m[![]() +
+![]() ],若存在,求m的值;若不存在,说明理由.
],若存在,求m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
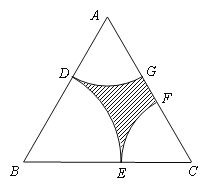
【题目】近年来,随着我市经济的快速发展,政府对民生也越来越关注. 市区现有一块近似正三角形土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形DBE,DAG和ECF,其中![]() 、
、![]() 与
与![]() 分别相切于点D、E,且
分别相切于点D、E,且![]() 与
与![]() 无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
(1)试用x分别表示扇形DAG和DBE的面积,并写出x的取值范围;
(2)当x为何值时,草坪面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.两条相交直线在同一平面内的射影必为相交直线
B.不共线三点到平面![]() 的距离相等,则这三点确定的平面不一定与平面
的距离相等,则这三点确定的平面不一定与平面![]() 平行
平行
C.对确定的两异面直线,过空间任一点有且只有一个平面与两异面直线都平行
D.两个相交平面的交线是一条线段
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当我们所处的北半球为冬季的时候,新西兰的惠灵顿市恰好是盛夏,因此北半球的人们冬天愿意去那里旅游,下面是一份惠灵顿机场提供的月平均气温统计表.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 17.3 | 17.9 | 17.3 | 15.8 | 13.7 | 11.6 | 10.06 | 9.5 | 10.06 | 11.6 | 13.7 | 15.8 |
(1)根据这个统计表提供的数据,为惠灵顿市的月平均气温作出一个函数模型;
(2)当自然气温不低于13.7℃时,惠灵顿市最适宜旅游,试根据你所确定的函数模型,确定惠灵顿市的最佳旅游时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,加快水污染防治,建设美丽中国.根据环保部门对某河流的每年污水排放量![]() (单位:吨)的历史统计数据,得到如下频率分布表:
(单位:吨)的历史统计数据,得到如下频率分布表:

将污水排放量落入各组的频率作为概率,并假设每年该河流的污水排放量相互独立.
(1)求在未来3年里,至多1年污水排放量![]() 的概率;(2)该河流的污水排放对沿河的经济影响如下:当
的概率;(2)该河流的污水排放对沿河的经济影响如下:当![]() 时,没有影响;当
时,没有影响;当![]() 时,经济损失为10万元;当
时,经济损失为10万元;当![]() 时,经济损失为60万元.为减少损失,现有三种应对方案:
时,经济损失为60万元.为减少损失,现有三种应对方案:
方案一:防治350吨的污水排放,每年需要防治费3.8万元;
方案二:防治310吨的污水排放,每年需要防治费2万元;
方案三:不采取措施.
试比较上述三种文案,哪种方案好,并请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com