
如图1,在△ABC中,BC=3,AC=6,∠C=90°,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2。

(1)求证:BC⊥平面A1DC;
(2)若CD=2,求BE与平面A1BC所成角的正弦值。
(1)详见解析;(2)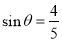
【解析】
试题分析:(1)可以利用线线BC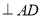 ,
,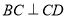 垂直,来证明线面BC⊥平面A1DC垂直;
垂直,来证明线面BC⊥平面A1DC垂直;
(2)可以以D为原点,分别以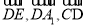 为x,y,z轴的正方向,建立空间直角坐标系,然后利用空间向量的线面角公式
为x,y,z轴的正方向,建立空间直角坐标系,然后利用空间向量的线面角公式 即可.
即可.
试题解析:(Ⅰ) DE
DE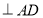 ,DE//BC,
,DE//BC, BC
BC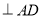 2分
2分
又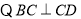 ,AD
,AD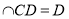
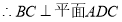 4分
4分
(2)以D为原点,分别以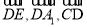 为x,y,z轴的正方向,
为x,y,z轴的正方向,
建立空间直角坐标系D-xyz 5分
说明:建系方法不唯一 ,不管左手系、右手系只要合理即可
在直角梯形CDEB中,过E作EF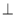 BC,EF=2,BF=1,BC=3 6分
BC,EF=2,BF=1,BC=3 6分
 B(3,0,-2)E(2,0,0)C(0,0,-2)A1(0,4,0) 8分
B(3,0,-2)E(2,0,0)C(0,0,-2)A1(0,4,0) 8分
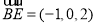
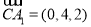
 9分
9分
设平面A1BC的法向量为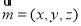

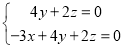
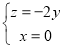 令y=1,
令y=1,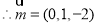 10分
10分
设BE与平面A1BC所成角为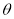 ,
,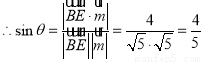 12分
12分
考点:(1)空间位置关系的证明;(2)利用向量解决立体几何问题.


科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:选择题
如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器厚度,则球的体积为( )

A. cm3 B.
cm3 B. cm3
cm3
C. cm3 D.
cm3 D.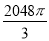 cm3
cm3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 数列、推理与证明(解析版) 题型:选择题
(2013·课标全国卷Ⅱ)等比数列{an}的前n项和为Sn,已知S3=a2+10a1,a5=9,则a1=( )
A. B.-
B.- C.
C. D.-
D.-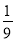
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量(解析版) 题型:选择题
设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,则角C=( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年吉林省延边州高考复习质量检测文科数学试卷(解析版) 题型:选择题
关于x的方程ex-1-|kx|=0(其中e=2.71828…是自然对数的底数)的有三个不同实根,则k的取值范围是
A.{-2,0,2} B.(1,+∞) C.{k|k>e} D.{k|k2>1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com