练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器厚度，则球的体积为(　　)

    A. cm3 B. cm3

    C. cm3 D. cm3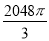

     

    A

    【解析】如图，作出球的一个截面，则MC＝8－6＝2(cm)，BM＝AB＝×8＝4(cm)．设球的半径为R cm，则R2＝OM2＋MB2＝(R－2)2＋42，

    ∴R＝5，

    ∴V球＝π×53＝π(cm3)．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学人教版评估检测 第七章 立体几何（解析版） 题型：填空题

    如图所示,正四棱锥P-ABCD的底面积为3,体积为,E为侧棱PC的中点,则PA与BE所成的角为__________.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 解析几何（解析版） 题型：填空题

    执行如图所示的程序框图，若输入n的值为4，则输出s的值为________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：解答题

    如图，三棱柱ABC—A1B1C1的侧面AA1B1B为正方形，侧面BB1C1C为菱形，∠CBB1＝60°，AB⊥B1C.

    (1)求证：平面AA1B1B⊥平面BB1C1C；

    (2)若AB＝2，求三棱柱ABC—A1B1C1的体积．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：填空题

    已知函数f(x)＝Asin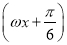(A＞0，ω＞0)的最小正周期为2，且f(0)＝，则函数f(3)＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：选择题

    在△ABC中，已知||＝||＝||＝2，则向量·＝(　　)

    A．2　　　B．－2　　　C．2　　　D．－2

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 概率与统计（解析版） 题型：填空题

    已知向量a＝(x，－1)，b＝(3，y)，其中x随机选自集合{－1,1,3}，y随机选自集合{1,3}，那么a⊥b的概率是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 数列、推理与证明（解析版） 题型：解答题

    (2013·安徽高考)设数列{an}满足a1＝2，a2＋a4＝8，且对任意n∈N*，函数f(x)＝x＋an＋1cos x－an＋2sin x满足f′＝0．

    (1)求数列{an}的通项公式；

    (2)若bn＝2，求数列{bn}的前n项和Sn．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年吉林省延边州高考复习质量检测理科数学试卷（解析版） 题型：解答题

    如图1，在△ABC中，BC=3，AC=6，∠C=90°，且DE∥BC，将△ADE沿DE折起到△A1DE的位置，使A1D⊥CD，如图2。

    （1）求证：BC⊥平面A1DC；

    （2）若CD=2，求BE与平面A1BC所成角的正弦值。

     

    查看答案和解析>>

    同步练习册答案