
如图所示,正四棱锥P-ABCD的底面积为3,体积为 ,E为侧棱PC的中点,则PA与BE所成的角为__________.
,E为侧棱PC的中点,则PA与BE所成的角为__________.

科目:高中数学 来源:2014年高考数学人教版评估检测 第五章 数列(解析版) 题型:选择题
数列{an}中,a1=1,对所有的n≥2,都有a1·a2·a3·…·an=n2,则a3+a5等于( )
A.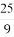 B.
B.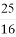 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第三章 三角函数、解三角形(解析版) 题型:解答题
(2014·孝感模拟)已知函数f(x)= sinωxcosωx-cos2ωx,其中ω为使f(x)能在x=
sinωxcosωx-cos2ωx,其中ω为使f(x)能在x= 时取得最大值的最小正整数.
时取得最大值的最小正整数.
(1)求ω的值.
(2)设△ABC的三边长a,b,c满足b2=ac,且边b所对的角θ的取值集合为M,当x∈M时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第三章 三角函数、解三角形(解析版) 题型:选择题
(2014 ·宜昌模拟)在△ABC中,若
·宜昌模拟)在△ABC中,若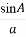 =
=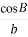 ,则B的值为( )
,则B的值为( )
A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:解答题
(2014·海淀模拟)如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.

(1)求证:A1B∥平面AEC1.
(2)求证:B1C⊥平面AEC1.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:选择题
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )
A.22πR2 B. πR2 C.
πR2 C. πR2 D.
πR2 D. πR2
πR2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:选择题
用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )
A. B.
B.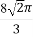 C.8
C.8 π D.
π D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:选择题
设f(x)= ,则不等式f(x)<2的解集为( )
,则不等式f(x)<2的解集为( )
A.(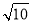 ,+∞) B.(-∞,1)∪[2,
,+∞) B.(-∞,1)∪[2,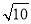 )
)
C.(1,2]∪(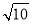 ,+∞) D.(1,
,+∞) D.(1,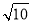 )
)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:选择题
如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器厚度,则球的体积为( )

A. cm3 B.
cm3 B. cm3
cm3
C. cm3 D.
cm3 D.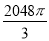 cm3
cm3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com