
【题目】如图,圆![]() ,点
,点![]() ,
,![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线和半径
的垂直平分线和半径![]() 相交于点
相交于点![]() .
.
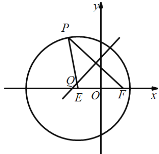
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)曲线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴上方),且
轴上方),且![]() .点
.点![]() ,
,![]() 是曲线
是曲线![]() 上位于直线
上位于直线![]() 两侧的两个动点,且
两侧的两个动点,且![]() .求四边形
.求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(1)![]()
(2)![]()
【解析】
(1)连接![]() ,根据题意可得
,根据题意可得![]() ,可得动点
,可得动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,则方程求可;
的椭圆,则方程求可;
(2)由![]() ,所以
,所以![]() ,设直线
,设直线![]() ,联立
,联立 ,利用韦达定理得
,利用韦达定理得![]() ,同理得
,同理得![]() ,设四边形
,设四边形![]() 面积为
面积为![]() ,可得
,可得![]() ,求其范围即可.
,求其范围即可.
(1)连接![]() ,
,
根据题意![]() ,则
,则![]() ,
,
故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,设其方程为
的椭圆,设其方程为![]() ,
,
可知![]() ,
,![]() ,则
,则![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ,
,
故椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)由题意可知,直线![]() ,直线
,直线![]() 的斜率都存在且不等于0,
的斜率都存在且不等于0,
因为![]() ,所以
,所以![]() ,
,
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() ,
,
设![]() ,
,
由 得
得![]() ①
①
依题意,方程①有两个不相等的实数根,即根的判别式![]() 成立,
成立,
即![]() ,
,
化简得![]() ,解得
,解得![]() ,
,
因为2是方程①的一个解,所以![]() ,
,
所以![]() ,
,
当方程①的判别式![]() 时,
时,![]() ,此时直线
,此时直线![]() 与椭圆相切,
与椭圆相切,
由题意,可知直线![]() 的方程为
的方程为![]() ,
,
同理,易得![]() ,
,
由于点![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的两个动点,
两侧的两个动点,![]() ,
,
且能存在四边形![]() ,则直线
,则直线![]() 的斜率
的斜率![]() 需满足
需满足![]() ,
,
设四边形![]() 面积为
面积为![]() ,则
,则![]()
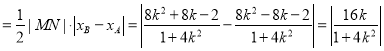 ,
,
由于![]() ,故
,故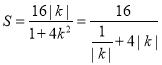 ,
,
当![]() 时,
时,![]() ,即
,即 ,即
,即![]() .
.
所以四边形![]() 面积
面积![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学将100名高一新生分成水平相同的甲,乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲,乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下,计成绩不低于90分者为“成绩优秀”.

(1)从乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的两个均“成绩优秀”的概率;
(2)由以上统计数据填写下面2x2列联表,并判断是否有![]() 的把握认为“成绩优秀”与教学方式有关.
的把握认为“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附: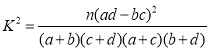
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | /tr>
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)定义![]() 为
为![]() ,
,![]() 两点所在直线的斜率,若四边形
两点所在直线的斜率,若四边形![]() 为椭圆的内接四边形,且
为椭圆的内接四边形,且![]() ,
,![]() 相交于原点
相交于原点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济水平及个人消费能力的提升,我国居民对精神层面的追求愈加迫切,如图是2007年到2017年我国城镇居民教育、文化、服务人均消费支出同比增速的折线图,图中显示2007年的同比增速为10%, 即2007年与2006年同时期比较2007年的人均消费支出费用是2006年的1.1倍.则下列表述中正确的是( )
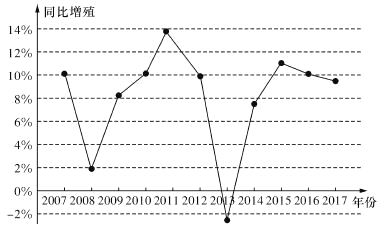
A.2007年到2017年,同比增速的中位数约为10%
B.2007年到2017年,同比增速的极差约为12%
C.2011年我国城镇居民教育、文化、服务人均消费支出的费用最高
D.2007年到2017年,我国城镇居民教育、文化、服务人均消费支出的费用逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:给定整数i,如果非空集合满足如下3个条件:
①![]() ;②
;②![]() ;③
;③![]() ,若
,若![]() ,则
,则![]() .
.
则称集合A为“减i集”
(1)![]() 是否为“减0集”?是否为“减1集”?
是否为“减0集”?是否为“减1集”?
(2)证明:不存在“减2集”;
(3)是否存在“减1集”?如果存在,求出所有“减1集”;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且椭圆上存在一点
,且椭圆上存在一点![]() ,满足
,满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,求
,求![]() 的内切圆的半径的最大值.
的内切圆的半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线![]() ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
A.0B.![]() C.
C.![]() -1D.
-1D.![]() +1
+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com