
分析 (1)分类讨论解不等式,可得M;
(2)利用反证法,即可证明.
解答 (1)解:x<3.5时,不等式化为4-x+2x-7>$\frac{1}{3}$(x-7),解得x>1,∴1<x<3.5;
3.5≤x<4时,不等式化为4-x-2x+7>$\frac{1}{3}$(x-7),解得x<4,∴3.5≤x<4;
x≥4时,不等式化为x-4-2x+7>$\frac{1}{3}$(x-7),解得x<4,无解;
综上所述,M={x|1<x<4};
(2)证明:要证明|$\sqrt{ab}$-2|<|2$\sqrt{a}$-$\sqrt{b}$|,
只要证明ab-4$\sqrt{ab}$+4<4a-4$\sqrt{ab}$+b,
只要证明ab+4<4a+b,
只要证明ab+4<4a+b,
只要证明(a-1)(b-4)<0,
∵a、b∈M={x|1<x<4},∴结论成立.
点评 本题考查不等式的解法与证明,考查分析法的运用,考查分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 第3项 | B. | 第4项 | C. | 第5项 | D. | 第6项 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 种植地编号 | A | B | C | D | E |
| (x,y,z) | (1,0,0) | (2,2,1) | (0,1,1) | (2,0,2) | (1,1,1) |
| 种植地编号 | F | G | H | I | J |
| (x,y,z) | (1,1,2) | (2,2,2) | (0,0,1) | (2,2,1) | (0,2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 9 | C. | 8 | D. | $\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
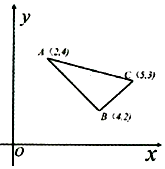 已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )
已知点(x,y)在△ABC所包围的阴影区域内(包括边界),若有且仅有B(4,2)是使得z=ax-y取得最大值的最优解,则实数a的取值范围为( )| A. | -1<a<1 | B. | -1≤a≤1 | C. | -1≤a<1 | D. | -1<a≤1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com