Question

11．用大小完全相同的黑、白两种颜色的正六边形积木拼成如图所示的图案，按此规律再拼5个图案，并将这8个图案中的所有正六边形积木充分混合后装进一个盒子中，现从盒子中随机取出一个积木，则取出黑色积木的概率是$\frac{9}{49}$．

Answer 1

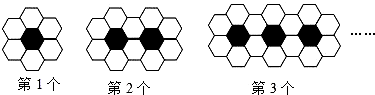
分析 由图形可知各图形中的黑色积木和白色积木分别成等差数列，求出积木总个数，使用古典概型的概率计算公式计算概率．

解答 解：由图可知第1个图形由1个黑色积木，6个白色积木，第二个图形有2个黑色积木，10个白色积木，第三个图形有3个黑色积木，14个白色积木，
依此类推，故图形中的黑色积木数组成一个等差数列，公差为1，白色积木数组成一个等差数列，公差为4．
从而前8个图形共有黑色积木个数为8×1+$\frac{8×7}{2}×1$=36，共有白色积木个数为8×6+$\frac{8×7}{2}×4$=160．
∴取出黑色积木的概率P=$\frac{36}{36+160}$=$\frac{9}{49}$．
故答案为$\frac{9}{49}$．

点评 本题考查了归纳推理，古典概型的概率计算，属于基础题．