
在产品质量检验时,常从产品中抽出一部分进行检查.现在从98件正品和2件次品共100件产品中,任意抽出3件检查.
(1)共有多少种不同的抽法?
(2)恰好有一件是次品的抽法有多少种?
(3)至少有一件是次品的抽法有多少种?
(4)恰好有一件是次品,再把抽出的3件产品放在展台上,排成一排进行对比展览,共有多少种不同的排法?
(1)161700 (2)9506 (3)9604 (4)57036
【解析】
【解析】
(1)所求不同的抽法数,即从100个不同元素中任取3个元素的组合数,共有C1003=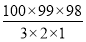 =161700(种).
=161700(种).
(2)抽出的3件中恰好有一件是次品这件事,可以分两步完成:
第一步,从2件次品中任取1件,有C21种方法;
第二步,从98件正品中任取2件,有C982种方法.
根据分步计数原理,不同的抽取方法共有
C21·C982=2×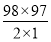 =9506(种).
=9506(种).
(3)法一 抽出的3件中至少有一件是次品这件事,分为两类:
第一类:抽出的3件中有1件是次品的抽法,有C21C982种;
第二类:抽出的3件中有2件是次品的抽法,有C21C981种.
根据分类计数原理,不同的抽法共有
C21·C982+C22·C981=9506+98=9604(种).
法二 从100件产品中任取3件的抽法,有C1003种,其中抽出的3件中没有次品的抽法,有C983种.所以抽出的3件中至少有一件是次品的抽法,共有C1003-C983=9604(种).
(4)完成题目中的事,可以分成两步:
第一步,选取产品,有C21C982种方法;
第二步,选出的3个产品排列,有A33种方法.
根据分步计数原理,不同的排列法共有
C21C982A33=57036(种).


科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.1练习卷(解析版) 题型:填空题
一袋中装有6个同样大小的黑球,编号为1,2,3,4,5,6.现从中随机地取出3个,用X表示取出的球的最大号码,则{X=6}表示的试验结果是________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.3练习卷(解析版) 题型:填空题
从甲、乙等10名同学中挑选4名参加某项公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有________种.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.3练习卷(解析版) 题型:填空题
已知集合A={1,2,3,4},B={5,6,7},C={8,9}.现在从这三个集合中取出两个集合,再从这两个集合中各取出一个元素,组成一个含有两个元素的集合 ,则一共可以组成集合的个数为________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.2练习卷(解析版) 题型:填空题
某商店要求甲、乙、丙、丁、戊五种不同的商品在货架上排成一排,其中甲、乙两种必须排在一起,而丙、丁两种不能排在一起,不同的排法共有________种.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1.1练习卷(解析版) 题型:解答题
某电视台连续播放6个广告,其中有3个不同的商业广告、两个不同的世博会宣传广告、一个公益广告,要求最后播放的不能是商业广告,且世博会宣传广告与公益广告不能连续播放,两个世博会宣传广告也不能连续播放,则有多少种不同的播放方式?
查看答案和解析>>
科目:高中数学 来源:2015届福建省龙岩市高二上学期教学质量检查理科数学试卷(解析版) 题型:选择题
下列命题正确的是
A. “ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件
B. 对于命题p: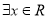 ,使得
,使得 ,则
,则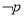 :
: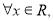 均有
均有
C. 若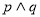 为假命题,则
为假命题,则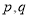 均为假命题
均为假命题
D. 命题“若 ,则
,则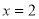 ”的否命题为“若
”的否命题为“若 则
则
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com