
| A. | (-∞,-6)∪(6,+∞) | B. | (-∞,-4)∪(4,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-1)∪(1,+∞) |
分析 由$f({x_0})=±\sqrt{3}$,[f(x0)]2=3,求导,令f′(x0)=0,求得$\frac{{x}_{0}}{m}$=k+$\frac{1}{2}$,即可求得丨x0丨≥丨$\frac{m}{2}$丨,即x${\;}_{0}^{2}$+[f(x0)]2≥$\frac{{m}^{2}}{4}$+3,由x${\;}_{0}^{2}$+[f(x0)]2<m2,求得m2>$\frac{{m}^{2}}{4}$+3,求得m的取值范围.
解答 解:由题意知:$f({x_0})=±\sqrt{3}$,
∴[f(x0)]2=3,
∵f′(x0)=$\frac{π}{m}$•$\sqrt{3}$cos$\frac{π{x}_{0}}{m}$=0,
∴$\frac{π{x}_{0}}{m}$=kπ+$\frac{π}{2}$,(k∈Z),
∴$\frac{{x}_{0}}{m}$=k+$\frac{1}{2}$,(k∈Z),即丨$\frac{{x}_{0}}{m}$丨=丨k+$\frac{1}{2}$丨≥$\frac{1}{2}$,
∴丨x0丨≥丨$\frac{m}{2}$丨,即x${\;}_{0}^{2}$+[f(x0)]2≥$\frac{{m}^{2}}{4}$+3,
而已知x${\;}_{0}^{2}$+[f(x0)]2<m2,
∴m2>$\frac{{m}^{2}}{4}$+3,
故$\frac{3{m}^{2}}{4}$>3,解得m>2或m<-2,
故答案选:C.
点评 本题考查正弦函数图象及性质,导数的运算,考查利用导数研究函数的极值,不等式的解法,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{7}{9}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
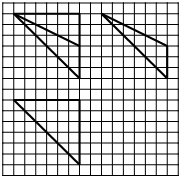 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,则该零件的表面积为(单位:cm2)( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,则该零件的表面积为(单位:cm2)( )| A. | $27\sqrt{2}+9\sqrt{5}+9$ | B. | $27\sqrt{2}+18\sqrt{5}$ | C. | $9\sqrt{2}+9\sqrt{5}+27$ | D. | $36+9\sqrt{5}+18\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 第4天 | 第8天 | 第16天 | 第22天 |
| 价格(元) | 23 | 24 | 22 | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com