
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①③④ |
分析 作出正方体ABCD-A1B1C1D1,利用正方体的结构特征,结合题设条件,能够作出正确判断.
解答 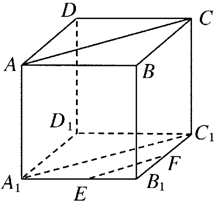 解:如图所示.由于AA1⊥平面A1B1C1D1,EF?平面A1B1C1D1,
解:如图所示.由于AA1⊥平面A1B1C1D1,EF?平面A1B1C1D1,
则EF⊥AA1,所以①正确;
由于平面A1B1C1D1∥平面ABCD,EF?平面A1B1C1D1,
所以EF∥平面ABCD,所以②正确.
当E,F分别不是线段A1B1,B1C1的中点时,EF与AC异面,
所以③不正确;
当E,F分别是线段A1B1,B1C1的中点时,EF∥A1C1,又AC∥A1C1,
则EF∥AC,所以AC∥面EFB,所以④正确;
故选:C.
点评 本题考查线线、线面位置关系,解题的关键是利用面面位置关系判断线线、线面位置关系,属于中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:选择题
| A. | 平行于同一直线的两直线平行 | |
| B. | 垂直于同一直线的两直线平行 | |
| C. | 平行于同一平面的两平面不一定平行 | |
| D. | 垂直于同一平面的两平面平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 31 | C. | 30 | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-6)∪(6,+∞) | B. | (-∞,-4)∪(4,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 3+2$\sqrt{2}$ | C. | 3+$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
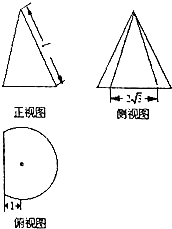 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为2$\sqrt{2}$.
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com