
����Ŀ��ij�о�С���ڵ����Ͻ����˹�����ģ��ʵ�飬����![]() ��
��![]() ��
��![]() �����˹����귽ʽ�ֱ�Լס��ҡ�������ʵʩ�˹����꣬����������ͳ�������
�����˹����귽ʽ�ֱ�Լס��ҡ�������ʵʩ�˹����꣬����������ͳ�������
��ʽ | ʵʩ�ص� | ���� | ���� | С�� | ģ��ʵ���ܴ��� |
| �� | 4�� | 6�� | 2�� | 12�� |
| �� | 3�� | 6�� | 3�� | 12�� |
| �� | 2�� | 2�� | 8�� | 12�� |
�ٶ��Լס��ҡ�������ʵʩ���˹�����˴˻���Ӱ�죬��������˹�����ģ��ʵ���ͳ�����ݣ�
������ס��ҡ������ض�ǡΪ����ĸ��ʣ�
�����ǵ������ˮ����ʧ�������ǡ�����꼴�ﵽ����״̬���ҵر����Ǵ���Ŵﵽ����״̬������ֻ����С������꼴�ﵽ����״̬���ǡ��ס��ҡ��������дﵽ����״̬�ĸ�����Ϊ�������![]() �����������
�����������![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() ��
��
���𰸡���1��![]() ����2���ֲ��м���������ѧ����
����2���ֲ��м���������ѧ����![]() .
.
�������������������1�����˹�����ģ��ʵ���ͳ�����ݣ���![]() ��
��![]() ��
��![]() �����˹����귽ʽ�ֱ�Լס��ҡ�������ʵʩ�˹����꣬������ꡢ���ꡢС��ĸ��ʷֲ���,������������¼����ʼ��㹫ʽ������ض�Ϊ����ĸ��ʣ���2��
�����˹����귽ʽ�ֱ�Լס��ҡ�������ʵʩ�˹����꣬������ꡢ���ꡢС��ĸ��ʷֲ���,������������¼����ʼ��㹫ʽ������ض�Ϊ����ĸ��ʣ���2��![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ,
,![]() ,
,![]() ,
,![]() ���ֱ����
���ֱ����![]() ȡ�⼸��ֵʱ�ĸ���,������ֲ��к���ѧ����.
ȡ�⼸��ֵʱ�ĸ���,������ֲ��к���ѧ����.
�����������1�����˹�����ģ��ʵ���ͳ�����ݣ���![]() ��
��![]() ��
��![]() �����˹����귽ʽ�ֱ�Լס��ҡ�������ʵʩ�˹����꣬�õ����ꡢ���ꡢС��ĸ������±���
�����˹����귽ʽ�ֱ�Լס��ҡ�������ʵʩ�˹����꣬�õ����ꡢ���ꡢС��ĸ������±���
��ʽ | ʵʩ�ص� | ���� | ���� | С�� |
| �� |
|
|
|
| �� |
|
|
|
| �� |
|
|
|
�����ס��ҡ������ض�ǡΪ������Ϊ�¼�![]() ����
����
![]() ��
��
��2����ס��ҡ������شﵽ����״̬�ĸ��ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
![]() �Ŀ���ȡֵΪ0,1,2,3��
�Ŀ���ȡֵΪ0,1,2,3��
![]() ��
��
![]()
![]() ��
��
![]()
![]() ��
��
![]() ��
��
�����������![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 0 | 1 | 2 | 3 |
|
|
|
|
|
��ѧ����![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��
����![]() ��������
��������![]() ����������С������Ϊ
����������С������Ϊ![]() ��
��
����ͨ��ѧֻ��1��2�ʣ�
��1����![]() ��ֵ�����������
��ֵ�����������![]() �ĵ����������䣻
�ĵ����������䣻
��2����![]() ������
������![]() ��ʱ���Ǻ���
��ʱ���Ǻ���![]() �����ֵ����Сֵ��
�����ֵ����Сֵ��
��Ϊ![]() ��
��![]() ����
����![]() ������
������![]() �Ľ�
�Ľ�
��ʽ��
��3���ڵڣ�2���ʵ�ǰ���£���֪����![]() ��
�� ![]() ������������
������������![]() ��
�� ![]() ���ܴ���
���ܴ���![]() ��ʹ��
��ʹ��![]()
![]() ��������ʵ��t��ȡֵ��Χ.
��������ʵ��t��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ100��ѧ�����п�����ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ�����гɼ������������£�
��� | ��һ�� | �ڶ��� | ������ | ������ | ������ |
���� | [50��60�� | [60��70�� | [70��80�� | [80��90�� | [90��100] |
��1����ͼ��a��ֵ��
��2������Ƶ�ʷֲ�ֱ��ͼ��������100��ѧ�����п�����ѧ�ɼ���ƽ���֣�
��3�����÷ֲ�����ķ����ӵ�3��4��5���������ȡ6��ѧ����������������һ�����壬���������ȡ2����������ǡ��1�˵ķ���������90�ֵĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ������
������![]() ��ֱ��
��ֱ��![]() ��Բ
��Բ![]() ���У���
������![]() ��
��![]() �ģ� ��
�ģ� ��
A. ��ֱ�Ҫ���� B. ��Ҫ���������
C. ��ֲ���Ҫ���� D. �Ȳ����Ҳ����Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij�˶�Աÿ��Ͷ�����еĸ��ʵ���![]() ���ֲ������ģ��ķ������Ƹ��˶�Ա����Ͷ��ǡ���������еĸ��ʣ����ɼ���������0��9֮��ȡ����ֵ���������ָ��1��2��3��4��ʾ���У�5��6��7��8��9��0��ʾ�����У�����ÿ���������Ϊһ�飬��������Ͷ���Ľ���������ģ�����������20���������
���ֲ������ģ��ķ������Ƹ��˶�Ա����Ͷ��ǡ���������еĸ��ʣ����ɼ���������0��9֮��ȡ����ֵ���������ָ��1��2��3��4��ʾ���У�5��6��7��8��9��0��ʾ�����У�����ÿ���������Ϊһ�飬��������Ͷ���Ľ���������ģ�����������20���������
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
�ݴ˹��ƣ����˶�Ա����Ͷ��ǡ���������еĸ���Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4��4������ϵ���������
��ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ ��
��![]() Ϊ������.��ԭ��Ϊ���㣬
Ϊ������.��ԭ��Ϊ���㣬![]() ��������Ϊ���Ὠ��������ϵ��Բ
��������Ϊ���Ὠ��������ϵ��Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
������д��ֱ��![]() ����ͨ���̺�Բ
����ͨ���̺�Բ![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
����������![]() ��ֱ������Ϊ
��ֱ������Ϊ![]() ��Բ
��Բ![]() ��ֱ��
��ֱ��![]() ����
����![]() ���㣬��
���㣬��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ������������ˮ�أ����ݻ�Ϊ6400�����ף����Ϊ4�ף��ص�ÿƽ�������Ϊ120Ԫ���ر�ÿƽ�������Ϊ100Ԫ����ص׳����εij�Ϊx�ף�
�����������������ú�x�ı���ʽ��ʾ�ر������
�������������ˮ����ʹ��������?�������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⳤΪ1��������ABCD��A1B1C1D1�У�
M��N�ֱ���AB1��BC1���е�.
������֤��ֱ��MN//ƽ��ABCD.
������B1��ƽ��A1BC1�ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�ĵ���Ϊƽ���ı��Σ�PD��ƽ��ABCD��MΪPC�е㣮
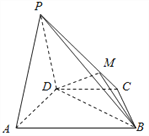
��1����֤��AP��ƽ��MBD��
��2����AD��PB����֤��BD��ƽ��PAD��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com