
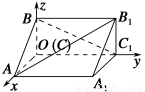
如图,在空间直角坐标系中有直三棱柱ABC ?A1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( ).
A. B.
B.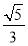 C.
C.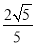 D.
D.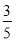
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练7练习卷(解析版) 题型:填空题
若α,β∈ ,cos
,cos 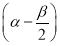 =
= ,sin
,sin 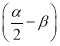 =-
=-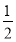 ,则cos (α+β)=________.
,则cos (α+β)=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练15练习卷(解析版) 题型:解答题
已知椭圆C的中心为平面直角坐标系xOy的原点,焦点在x轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆C的方程;
(2)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的一点,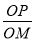 =λ,求点M的轨迹方程,并说明轨迹是什么曲线.
=λ,求点M的轨迹方程,并说明轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:选择题
已知圆的方程为x2+y2-6x-8y=0,设该圆中过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是( ).
A.10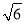 B.20
B.20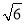 C.30
C.30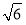 D.40
D.40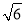
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:填空题
已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连接DM,则DM与平面PAC所成角的大小是________.
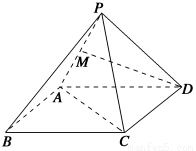
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:解答题
如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB= EF.
EF.

(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
已知α,β,γ是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①a∥γ,b?β;②a∥γ,b∥β;③b∥β,a?γ.如果命题“α∩β=a,b?γ,且________,那么a∥b”为真命题,则可以在横线处填入的条件是( ).
A.①或② B.②或③ C.①或③ D.只有②
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:填空题
观察下列等式
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
……
照此规律,第n个等式可为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:解答题
已知数列{an}的前n项和是Sn,且Sn+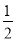 an=1.
an=1.
(1)求数列{an}的通项公式;
(2)记bn=log3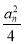 ,数列
,数列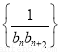 的前n项和为Tn,证明:Tn<
的前n项和为Tn,证明:Tn<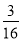 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com