Question

已知椭圆

x2

3

+

y2

2

=1的左右焦点分别为F₁、F₂，过F₁的直线交椭圆于B、D两点，过F₂的直线交椭圆于A、C两点，且AC⊥BD，垂足为P
（Ⅰ）设P点的坐标为（x₀，y₀），证明：

x02

3

+

y02

2

＜1；
（Ⅱ）求四边形ABCD的面积的最小值．

Answer 1

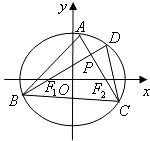
分析：（Ⅰ）椭圆的半焦距c=

3-2

=1，由AC⊥BD知点P在以线段F₁F₂为直径的圆上，故x₀²+y₀²=1，由此可以证出

x02

3

+

y02

2

＜1．
（Ⅱ）设BD的方程为y=k（x+1），代入椭圆方程

x2

3

+

y2

2

=1，并化简得（3k²+2）x²+6k²x+3k²-6=0．设B（x₁，y₁），D（x₂，y₂），由题意知|BD|=

1+k2

•|x1-x2|=

(1+k2)•[(x2+x2)2-4x1x2]

=

4 3 (k2+1)

3k2+2

再求出|AC|=

4 3 ( 1 k2 +1)

3× 1 k2 +2

=

4 3 (k2+1)

2k2+3

，由此可以求出四边形ABCD的面积的最小值．

解答：证明：（Ⅰ）椭圆的半焦距c=

3-2

=1，
由AC⊥BD知点P在以线段F₁F₂为直径的圆上，故x₀²+y₀²=1，
所以，

x 2 0

3

+

y 2 0

2

≤

x 2 0

2

+

y 2 0

2

=

1

2

＜1．
（Ⅱ）（ⅰ）当BD的斜率k存在且k≠0时，BD的方程为y=k（x+1），
代入椭圆方程

x2

3

+

y2

2

=1，并化简得（3k²+2）x²+6k²x+3k²-6=0．
设B（x₁，y₁），D（x₂，y₂），则x1+x2=-

6k2

3k2+2

，x1x2=

3k2-6

3k2+2

|BD|=

1+k2

•|x1-x2|=

(1+k2)•[(x1+x2)2-4x1x2]

=

4 3 (k2+1)

3k2+2

；
因为AC与BC相交于点P，且AC的斜率为-

1

k

，
所以，|AC|=

4 3 ( 1 k2 +1)

3× 1 k2 +2

=

4 3 (k2+1)

2k2+3

．
四边形ABCD的面积S=

1

2

•|BD||AC|=

24(k2+1)2

(3k2+2)(2k2+3)

≥

24(k2+1)2

[ (3k2+2)+(2k2+3) 2 ]2

=

96

25

．
当k²=1时，上式取等号．
（ⅱ）当BD的斜率k=0或斜率不存在时，四边形ABCD的面积S=4．
综上，四边形ABCD的面积的最小值为

96

25

．

点评：本题综合考查椭圆的性质信其应用，难度较大，解题时要认真审题，仔细计算，注意公式的灵活运用，避免出现不应有的错误．