
分析 (1)利用分数指数幂的运算法则,求得要求式子的值.
(2)利用条件以及同角三角函数的基本关系,求得 tanα的值,可得 $\frac{{{{sin}^2}α+2{{cos}^2}α}}{sinα•cosα}$=$\frac{{tan}^{2}α+2}{tanα}$ 的值.
解答 解:(1)计算:${({2\frac{1}{4}})^{\frac{1}{2}}}-{({-9.6})^0}-{({3\frac{3}{8}})^{-\frac{2}{3}}}+{({1.5})^{-2}}+lg25+lg4+{7^{{{log}_7}2}}$
=$\frac{3}{2}$-1-$\frac{1}{{(\frac{27}{8})}^{\frac{2}{3}}}$+${(\frac{2}{3})}^{2}$+lg100+2
=$\frac{3}{2}$-1-$\frac{4}{9}$+$\frac{4}{9}$+2+2=$\frac{9}{2}$.
(2)∵已知sinα-2cosα=0,∴tanα=2,∴$\frac{{{{sin}^2}α+2{{cos}^2}α}}{sinα•cosα}$=$\frac{{tan}^{2}α+2}{tanα}$=$\frac{4+2}{2}$=3.
点评 本题主要考查分数指数幂的运算法则的应用,同角三角函数的基本关系,属于基础题.


科目:高中数学 来源: 题型:选择题
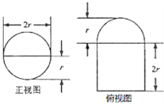 如图是一个圆柱被一个平面截去一部分后与半球(半径r=3)组成一个几何体,该几何图体三视中的正视图和俯视图如图所示,则该几何体的表面积为( )
如图是一个圆柱被一个平面截去一部分后与半球(半径r=3)组成一个几何体,该几何图体三视中的正视图和俯视图如图所示,则该几何体的表面积为( )| A. | 63π | B. | 80π | C. | 36+27π | D. | 36+45π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com