
若不等式ax2+bx+2>0的解集为- <x<
<x<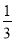 ,则不等式2x2+bx+a<0的解集是________.
,则不等式2x2+bx+a<0的解集是________.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:选择题
一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )
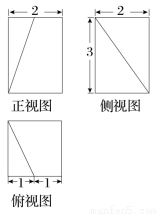
A.9 B.10 C.11 D.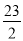
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-5合情推理与演绎推理(解析版) 题型:选择题
给出下面类比推理命题(其中Q为有理数集,R为实数集,C为复数集):
①“若a,b∈R,则a-b=0⇒a=b”,类比推出“若a,b∈C,则a-b=0⇒a=b”;
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”,类比推出,“若a,b,c,d∈Q,则a+b =c+d
=c+d ⇒a=c,b=d”;
⇒a=c,b=d”;
③“若a,b∈R,则a-b>0⇒a>b”,类比推出“若a,b∈C,则a-b>0⇒a>b”;
④“若x∈R,则|x|<1⇒-1<x<1”,类比推出“若z∈C,则|z|<1⇒-1<z<1”.
其中类比正确的为( )
A.①② B.①④ C.①②③ D.②③④
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-4基本不等式(解析版) 题型:选择题
若向量a=(x-1,2),b=(4,y)相互垂直,则9x+3y的最小值为( )
A.12 B.2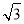 C.3
C.3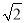 D.6
D.6
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:解答题
设二次函数f(x)=ax2+bx+c,函数F(x)=f(x)-x的两个零点为m,n(m<n).
(1)若m=-1,n=2,求不等式F(x)>0的解集;
(2)若a>0,且0<x<m<n<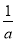 ,比较f(x)与m的大小.
,比较f(x)与m的大小.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-2一元二次不等式及其解法(解析版) 题型:选择题
不等式log2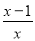 ≥1的解集为( )
≥1的解集为( )
A.(-∞,-1] B.[-1,+∞)
C.[-1,0) D.(-∞,-1]∪(0,+∞)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:6-1不等关系与不等式(解析版) 题型:解答题
已知关于x的不等式(ax-5)(x2-a)<0的解集为M.
(1)当a=4时,求集合M;
(2)当3∈M,且5∉M时,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-5数列的综合应用(解析版) 题型:选择题
各项都是正数的等比数列{an}的公比q≠1且a2, a3,a1成等差数列,则
a3,a1成等差数列,则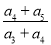 =( )
=( )
A.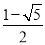 B.
B.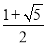
C.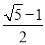 D.
D. 或
或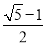
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:5-2等差数列及其前n项和(解析版) 题型:填空题
设等差数列{an}的前n项和为Sn,若S4=8,S8=20,则a11+a12+a13+a14=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com