
| A. | $f(x)=\sqrt{x^2}$与g(x)=x | B. | $f(x)={3^{{{log}_3}x}}$与g(x)=x | ||
| C. | f(x)=2-x与$g(x)={({\frac{1}{2}})^x}$ | D. | f(x)=|x-3|与g(x)=x-3 |
分析 要表示同一个函数,必须有相同的对应法则,相同的定义域,观察四个选项,得到有两组函数的对应法则不同,有一组函数的定义域不同,只有C选项,整理以后完全相同.
解答 解:对于A,f(x)=$\sqrt{{x}^{2}}$=|x|,g(x)=x,两函数的对应法则和值域不同,不为同一函数;
对于B,$f(x)={3^{{{log}_3}x}}$=x(x>0)与g(x)=x两函数的定义域不同,不为同一函数;
对于C,f(x)=2-x与$g(x)={({\frac{1}{2}})^x}$=2-x,两函数的对应法则和定义域相同,为同一函数;
对于D,f(x)=|x-3|与g(x)=x-3,两函数的对应法则和值域不同,不为同一函数.
故选:C.
点评 本题考查判断两个函数是否为同一个函数,这种题目一般从三个方面来观察,绝大部分题目是定义域不同,有一小部分是对应法则不同,只有极个别的是值域不同.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
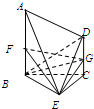 如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.
如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,F,G分别是AB,CD的中点.求证.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 实验顺序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
| 零件数 x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 66 | 75 | 84 | 88 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com