
如图所示,质点P在正方形ABCD的四个顶点上按逆时针方向前进,现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上所标数字分别为1、1、2、2、3、3.质点P从A点出发,规则如下:当正方体朝上一面出现的数字是1,质点P前进一步(如由A到B),当正方体朝上一面出现的数字是2,质点P前进两步(如由A到C);当正方体朝上一面出现的数字是3,质点P前进三步(如由A到D).在质点P转一圈之前连续投掷,若超过一圈,则投掷终止.
(1)求点P恰好返回到点A的概率;
(2)在点P转一圈恰能返回到点A的所有结果中,用随机变量ξ表示点P恰能返回到点A的投掷次数,求ξ的数学期望.
解:(1)事件“点P转一圈恰能返回到点A”记为M;事件“投掷两次点P就恰能返回到点A”记为B;事件“投掷三次点P就恰能返回到点A”记为D;事件“投掷四次点P就恰能返回到点A”记为E.投掷一次正方体玩具,朝上一面每个数字的出现都是等可能的,其概率为P1=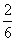 =
= ,因为只投掷一次不可能返回到点A;若投掷两次点P就恰能返回到点A,则朝上一面出现的两个数字应依次为:(1,3),(3,1),(2,2)三种结果,其概率为P(B)=
,因为只投掷一次不可能返回到点A;若投掷两次点P就恰能返回到点A,则朝上一面出现的两个数字应依次为:(1,3),(3,1),(2,2)三种结果,其概率为P(B)=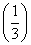 2×3=
2×3= ;
;
若投掷三次点P恰能返回到点A,则朝上一面出现的三个数字应依次为:
(1,1,2),(1,2,1),(2,1,1)三种结果,其概率为P(D)=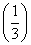 3×3=
3×3=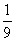 ;
;
若投掷四次点P恰能返回到点A,则朝上一面出现的四个数字应依次为:
(1,1,1,1),其概率为P(E)=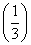 4=
4=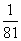 ;
;
所以点P恰好返回到点A的概率为
P(M)=P(B)+P(D)+P(E)= +
+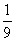 +
+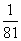 =
= .
.
(2)随机变量ξ的可能取值为2,3,4.
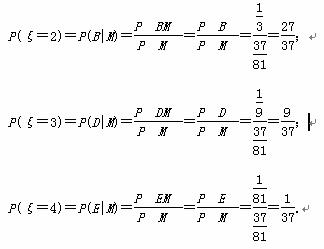 即ξ的分布列为
即ξ的分布列为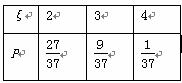 所以E(ξ)=2×
所以E(ξ)=2×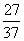 +3×
+3×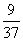 +4×
+4×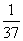 =
=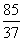 .即ξ的数学期望是
.即ξ的数学期望是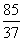 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知 中,
中, 的对边分别为
的对边分别为 且
且
(1)判断△ 的形状,并求
的形状,并求 的取值范围;
的取值范围;
(2)如图,三角形ABC的顶点 分别在l1、l2上运动,
分别在l1、l2上运动, 若直线l1
若直线l1 直线l2 ,且相交于点O,求
直线l2 ,且相交于点O,求 间距离的取值范围.
间距离的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
某次知识竞赛规则如下:在主办方预设的5个问题中,选手若能连续正确回答出两个问题,即停止答题,晋级下一轮.假设某选手正确回答每个问题的概率都是0.8,且每个问题的回答结果相互独立,则该选手恰好回答了4个问题就晋级下一轮的概率等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
曲线C1的极坐标方程ρcos2θ=sin θ,曲线C2的参数方程为 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为________.
,以极点为原点,极轴为x轴正半轴建立直角坐标系,则曲线C1上的点与曲线C2上的点最近的距离为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sin θ,ρcos =2
=2 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某商店每天(开始营业时)以每件15元的价格购入A商品若干(A商品在商店的保鲜时间为8小时,该商店的营业时间也恰好为8小时),并开始以每件30元的价格出售,若前6小时内所购进的A商品没有售完,则商店对没卖出的A商品将以每件10元的价格低价处理完毕(根据经验,2小时内完全能够把A商品低价处理完毕,且处理完毕后,当天不再购进A商品).该商店统计了100天A商品在每天的前6小时内的销售量,由于某种原因销售量频数表中的部分数据被污损而不能看清,制成如下表格(注:视频率为概率).
| 前6小时内的销售量X(单位:件) | 3 | 4 | 5 |
| 频数 | 30 | x | y |
(1)若某天商店购进A商品4件,试求商店该天销售A商品获取利润ξ的分布列和均值;
(2)若商店每天在购进4件A商品时所获得的平均利润最大,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
5名篮球运动员比赛前将外衣放在休息室,比赛后都回休息室取衣服.由于灯光暗淡,只有2人拿到自己的外衣,另外3人拿到别人外衣的情况有________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com