在直角坐标系xOy中，以O为极点，x轴正半轴为极轴建立极坐标系．圆C1，直线C2的极坐标方程分别为ρ＝4sin θ，ρcos
＝2
.
(1)求C1与C2交点的极坐标；
(2)设P为C1的圆心，Q为C1与C2交点连线的中点．已知直线PQ的参数方程为
(t∈R为参数)，求a，b的值．
口算题天天练系列答案科目：高中数学 来源： 题型：
已知函数f(x)＝
＋cos2x－sin2x.
(1)求函数f(x)的最小正周期和单调递减区间；
(2)在所给坐标系中画出函数在区间[
π，
π]的图像(只作图不写过程)．
查看答案和解析>>
科目：高中数学 来源： 题型：
如图所示，质点P在正方形ABCD的四个顶点上按逆时针方向前进，现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具，它的六个面上所标数字分别为1、1、2、2、3、3.质点P从A点出发，规则如下：当正方体朝上一面出现的数字是1，质点P前进一步(如由A到B)，当正方体朝上一面出现的数字是2，质点P前进两步(如由A到C)；当正方体朝上一面出现的数字是3，质点P前进三步(如由A到D)．在质点P转一圈之前连续投掷，若超过一圈，则投掷终止．
(1)求点P恰好返回到点A的概率；
(2)在点P转一圈恰能返回到点A的所有结果中，用随机变量ξ表示点P恰能返回到点A的投掷次数，求ξ的数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
设直线l1的参数方程为
(t为参数)，以坐标原点为极点，x轴非负半轴为极轴建立极坐标系，另一直线l2的方程为ρsin θ－3ρcos θ＋4＝0，若直线l1与l2间的距离为
，则实数a的值为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
设随机变量ξ～B(n，p)，且E(ξ)＝1.6，D(ξ)＝1.28，则( )
A．n＝8，p＝0.2 B．n＝4，p＝0.4
C．n＝5，p＝0.32 D．n＝7，p＝0.45
查看答案和解析>>
科目：高中数学 来源： 题型：
毕业生小王参加人才招聘会，分别向A，B两个公司投递个人简历．假定小王得到A公司面试的概率为
，得到B公司面试的概率为p，且两个公司是否让其面试是相互独立的．记ξ为小王得到面试的公司个数．若ξ＝0时的概率P(ξ＝0)＝
，则随机变量ξ的数学期望E(ξ)＝________.
查看答案和解析>>
科目：高中数学 来源： 题型：
某校高二(4)班组织学生报名参加国学社和摄影社，已知报名的每位学生至少报了一个社团，其中报名参加国学社的学生有2人，参加摄影社团的学生有5人，现从中选2人．设ξ为选出的学生中既报名参加国学社又报名参加摄影社的人数，且P(ξ>0)＝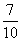
.
(1)求高二(4)班报名参加社团的学生人数；
(2)写出ξ的分布列并计算E(ξ)．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
x－
＋1.
解得a＝－1，b＝2.
, 且
,
, 求
的值．
B.36