
分析 将等式展开,利用数量积公式得到关于向量夹角的等式求之.
解答 解:由已知,|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$|=2,$\overrightarrow{b}$•($\overrightarrow{b}$+$\overrightarrow{a}$)=0,设夹角为α,所以${\overrightarrow{b}}^{2}+\overrightarrow{b}•\overrightarrow{a}=0$,所以1+2cosα=0,解答cosα=$-\frac{1}{2}$,
所以α=$\frac{2π}{3}$;
故答案为;$\frac{2π}{3}$.
点评 本题考查了向量的数量积于是以及利用数量积公式求夹角;属于基础题.


科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{6}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | (-1,3] | C. | (1,3] | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2枝玫瑰的价格高 | B. | 3枝康乃馨的价格高 | ||
| C. | 价格相同 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
在直角坐标系 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数,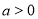 ),在以坐标原点为极点,
),在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 .
.
(1)求曲线 的普通方程,并将
的普通方程,并将 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)直线 的极坐标方程为
的极坐标方程为 ,其中
,其中 满足
满足 ,若曲线
,若曲线 与
与 的公共点都在
的公共点都在 上,求
上,求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com