
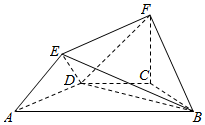
 如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,若CB=CD=CF=a.
如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,若CB=CD=CF=a.分析 (I)根据等腰三角形和等腰梯形性质可得∠ADB=90°,又BD⊥AE,得出BD⊥平面ADE,故而平面BDE⊥平面AED;
(II)VA-CDF=VF-ACD.
解答 证明:(Ⅰ)在等腰梯形ABCD中,
∵∠DAB=60°,∴∠CDA=∠DCB=120°
又∵CB=CD,
∴∠CDB=30°,
∴∠ADB=90°,即BD⊥AD.
又∵AE⊥BD,AE?平面ADE,AD?平面ADE,AD∩AE=A,
∴BD⊥平面AED,
又∵BD?平面BDE,
∴平面BDE⊥平面AED.
(Ⅱ)∵CB=CD=AD=a,∠ADC=120°,
∴S△ADC=$\frac{1}{2}×a×a×sin120°$=$\frac{\sqrt{3}{a}^{2}}{4}$,
∵FC⊥平面ABCD,且CF=a,
∴${V_{A-CDF}}={V_{F-ACD}}=\frac{1}{3}•{S_{△ACD}}•FC=\frac{{\sqrt{3}}}{12}{a^3}$,
∴三棱锥A-CDF的体积为$\frac{{\sqrt{3}}}{12}{a^3}$.
点评 本题考查了面面垂直的判定,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.
某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com