
 某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.
某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.分析 (1)先求出年龄在[35,40)之间的频率,由此能求出n,从而能求出第二组的频率,进而能求出第二组的矩形高,由此能补全频率分布直方图.
(2)由(1)知,[30,35)之间的人数为12,又[35,40)之间的人数为8,采用分层抽样抽取5人,其中[30,35)岁中有3人,[35,40)岁中有2人,由题意,随机变量ξ的甩有可能取值为1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 解:(1)年龄在[35,40)之间的频率为0.04×5=0.2,
∵$\frac{8}{n}$=0.2,∴n=$\frac{8}{0.2}$=40,
∵第二组的频率为:
1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,
∴第二组的矩形高为:$\frac{0.3}{5}$=0.06,
∴频率分布直方图如右图所示.
(2)由(1)知,[30,35)之间的人数为0.06×5×40=12,
又[35,40)之间的人数为8,
∵[30,35)岁年龄段人数与[35,40)岁年龄段人数的比值为12:8=3:2,
∴采用分层抽样抽取5人,其中[30,35)岁中有3人,[35,40)岁中有2人,
由题意,随机变量ξ的甩有可能取值为1,2,3,
P(ξ=1)=$\frac{{C}_{3}^{1}{C}_{2}^{2}}{{C}_{5}^{3}}$=$\frac{3}{10}$,
P(ξ=2)=$\frac{{C}_{3}^{2}{C}_{2}^{1}}{{C}_{5}^{3}}$=$\frac{3}{5}$,
P(ξ=3)=$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=$\frac{1}{10}$,
∴ξ的分布列为:
| ξ | 1 | 2 | 3 |
| P | $\frac{3}{10}$ | $\frac{3}{5}$ | $\frac{1}{10}$ |
点评 本题考查频率分布直方图的应用,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
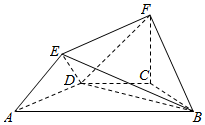 如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,若CB=CD=CF=a.
如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,若CB=CD=CF=a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,BD=4$\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点,且BE∥平面AGF.
如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,BD=4$\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点,且BE∥平面AGF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com