
分析 由|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥1,可得$|\overrightarrow{a}{|}^{2}+2\overrightarrow{a}•\overrightarrow{b}x+|\overrightarrow{b}{|}^{2}{x}^{2}$的最小值为1,令$\overrightarrow{a}•\overrightarrow{b}=t$换元,求出f(x)=4x2+2$\overrightarrow{a}•\overrightarrow{b}x$+4=4x2+2tx+4=$4(x+\frac{t}{4})^{2}+4-\frac{{t}^{2}}{4}$的最小值,由最小值大于等于1求得$\overrightarrow{a}$•$\overrightarrow{b}$的取值范围.
解答 解:由|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,由|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥1,可得$|\overrightarrow{a}{|}^{2}+2\overrightarrow{a}•\overrightarrow{b}x+|\overrightarrow{b}{|}^{2}{x}^{2}$的最小值大于等于1,
即4x2+2$\overrightarrow{a}•\overrightarrow{b}x$+4的最小值大于等于1.
令$\overrightarrow{a}•\overrightarrow{b}=t$,
则f(x)=4x2+2$\overrightarrow{a}•\overrightarrow{b}x$+4=4x2+2tx+4=$4(x+\frac{t}{4})^{2}+4-\frac{{t}^{2}}{4}$,
∵f(x)的最小值大于等于1,
∴$4-\frac{{t}^{2}}{4}≥1$,即t2≤12,
∴$-2\sqrt{3}≤t≤2\sqrt{3}$.
∴$\overrightarrow{a}$•$\overrightarrow{b}$的取值范围是[$-2\sqrt{3},2\sqrt{3}$].
故答案为:$[{-2\sqrt{3},2\sqrt{3}}]$.
点评 本题考查平面向量的数量积运算,考查数学转化思想方法,训练了利用配方法求函数的最值,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.
某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 将一个圆的八个等分点分成相间的两组,连接每组的四个点得到两个正方形.去掉两个正方形内部的八条线段后可以形成一正八角星,如图所示.设正八角星的中心为O,并且 $\overrightarrow{OA}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{OB}$=$\overrightarrow{{e}_{2}}$,若将点O到正八角星16个顶点的向量,都写成为λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$,λ,μ∈R的形式,则λ+μ的最大值为( )
将一个圆的八个等分点分成相间的两组,连接每组的四个点得到两个正方形.去掉两个正方形内部的八条线段后可以形成一正八角星,如图所示.设正八角星的中心为O,并且 $\overrightarrow{OA}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{OB}$=$\overrightarrow{{e}_{2}}$,若将点O到正八角星16个顶点的向量,都写成为λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$,λ,μ∈R的形式,则λ+μ的最大值为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 1+$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .1 | B. | .2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
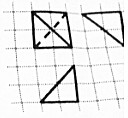 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一个四面体的三视图,则该四面体外接球的体积与四面体的体积的比值为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是一个四面体的三视图,则该四面体外接球的体积与四面体的体积的比值为( )| A. | 2$\sqrt{2}$π | B. | 3$\sqrt{3}$π | C. | 4π | D. | 2$\sqrt{5}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com