
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | -$\sqrt{3}$ |
分析 作出图形,将问题转化为解三角形问题.
解答 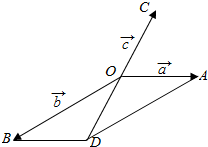 解:若$\overrightarrow a+\overrightarrow b+\overrightarrow c=\overrightarrow 0$,且$\overrightarrow a$与$\overrightarrow c$的夹角为60°,$\overrightarrow a$与$\overrightarrow b$的夹角为θ,$|{\overrightarrow b}|=\sqrt{3}|{\overrightarrow a}|$,
解:若$\overrightarrow a+\overrightarrow b+\overrightarrow c=\overrightarrow 0$,且$\overrightarrow a$与$\overrightarrow c$的夹角为60°,$\overrightarrow a$与$\overrightarrow b$的夹角为θ,$|{\overrightarrow b}|=\sqrt{3}|{\overrightarrow a}|$,
如图,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则∠COA=60°,以OA,OB为邻边作平行四边形OADB,
则 $\overrightarrow{OD}$=$\overrightarrow{a}$+$\overrightarrow{b}$=-$\overrightarrow{c}$,∠ODB=∠AOD=120°,BD=OA,OB=$\sqrt{3}$OA.
在△OBD中,由正弦定理得:$\frac{OB}{sin∠ODB}$=$\frac{BD}{sin∠BOD}$,∴$\frac{\sqrt{3}•OA}{\frac{\sqrt{3}}{2}}$=$\frac{OA}{sin∠BOD}$,
解得sin∠BOD=$\frac{1}{2}$,∴∠BOD=$\frac{π}{6}$,∴θ=∠BOD+∠AOD=$\frac{π}{6}$+$\frac{π}{3}$=$\frac{5π}{6}$,
∴tanθ=-$\frac{\sqrt{3}}{3}$.
故选:C.
点评 本题考查了平面向量加法的几何意义,正弦定理,属于中档题.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
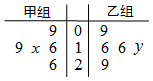 如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )| A. | 7、8 | B. | 5、7 | C. | 8、5 | D. | 7、7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com