
分析 $\overrightarrow{a}$,$\overrightarrow{b}$方向相反,可设$\overrightarrow{a}$=$λ\overrightarrow{b}$=(-3λ,4λ),(λ<0).再根据|$\overrightarrow{a}$|=5,利用数量积运算性质即可得出.
解答 解:∵$\overrightarrow{a}$,$\overrightarrow{b}$方向相反,
∴可设$\overrightarrow{a}$=$λ\overrightarrow{b}$=(-3λ,4λ),(λ<0).
∵|$\overrightarrow{a}$|=5,
∴5=$\sqrt{(-3λ)^{2}+(4λ)^{2}}$,
解得λ=-1,
∴$\overrightarrow{a}$=(3,-4).
故答案为:(3,-4).
点评 本题考查了向量共线定理、数量积运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | 0<a<1 | C. | a<-1或a>1 | D. | 1<a<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6,12,18 | B. | 7,11,19 | C. | 6,13,17 | D. | 7,12,17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{80π}{3}$ | B. | 32π | C. | 42π | D. | 48π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
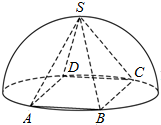 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为.( )
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{4\sqrt{2}}{3}$,则该半球的体积为.( )| A. | $\frac{4\sqrt{2}}{3}$π | B. | $\frac{8\sqrt{2}}{3}$π | C. | $\frac{32\sqrt{2}}{3}$π | D. | $\frac{64\sqrt{2}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
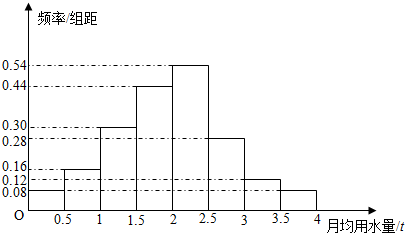
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com