
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
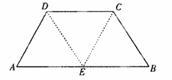
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点.将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
A.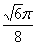 B.
B.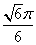 C.
C.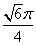 D.
D.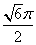
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数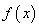 在R上可导,其导函数为
在R上可导,其导函数为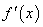 ,且函数
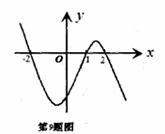
,且函数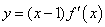 的图象如图所示,则关于函数
的图象如图所示,则关于函数 的下列结论,一定成立的是( )
的下列结论,一定成立的是( )
 A.
A.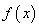 有极大值
有极大值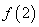 和极小值
和极小值
B.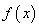 有极大值
有极大值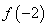 和极小值
和极小值
C.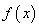 有极大值
有极大值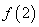 和极小值
和极小值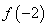
D.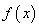 有极大值
有极大值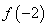 和极小值
和极小值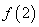
查看答案和解析>>
科目:高中数学 来源: 题型:
某超市一营业柜台销售某种商品,每件商品的成本为4元,并且每件商品需向超市交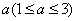 元的管理费,预计当诶吉安商品的售价为
元的管理费,预计当诶吉安商品的售价为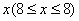 元时,一年的销售量为
元时,一年的销售量为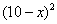 万件。
万件。
(1)求该营业柜台一年的利润L(万元)与每件商品的售价x的函数关系式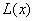 ;
;
(2)当每年商品的售价为多少元时,该营业柜台一年的利润L最大,并求出L的最大值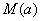 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
电视台应某企业之约播放两套连续剧。其中,连续剧甲每次播放时间为80分钟,其中广告时间为1分钟,收视观众为60万;连续剧乙每次播放时间为40分钟,广告时间为1分钟,收视观众为20万。已知此企业与电视台达成协议,要求电视台每周至少播放6分钟广告,而电视台每周只能为该企业提供不多于320分钟的节目时间。如果你是电视台的制片人,电视台每周应播映两套连续剧各多少次,才能获得最高的收视率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com