
【题目】给出以下结论:
①命题“若![]() ,则
,则![]() ”的逆否命题“若
”的逆否命题“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的充分条件;
”的充分条件;
③命题“若![]() ,则方程
,则方程![]() 有实根”的逆命题为真命题;
有实根”的逆命题为真命题;
④命题“若![]() ,则
,则![]() 且
且![]() ”的否命题是真命题.
”的否命题是真命题.
其中错误的是__________.(填序号)
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】某校学生会为了解该校学生对2017年全国两会的关注情况,随机调查了该校200名学生,并将这200名学生分为对两会“比较关注”与“不太关注”两类.已知这200名学生中男生比女生多20人,对两会“比较关注”的学生中男生人数与女生人数之比为![]() ,对两会“不太关注”的学生中男生比女生少5人.
,对两会“不太关注”的学生中男生比女生少5人.
(1)根据题意建立![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为男生与女生对两会的关注有差异?
的把握认为男生与女生对两会的关注有差异?
(2)该校学生会从对两会“比较关注”的学生中根据性别进行分层抽样,从中抽取7人,再从这7人中随机选出2人进行回访,求这2人全是男生的概率.
参考公式和数据:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不足120分的占![]() ,统计成绩后得到如下
,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | |||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)在上述样本中从分数不少于120分的学生中,按照分层抽样的方法,抽到线上学习时间不少于5小时和线上学习时间不足5小时的学生共5名,若在这5名学生中随机抽取2人,求至少1人每周线上学习时间不足5小时的概率.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式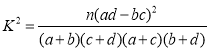 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两个研发小组,他们研究新产品成功的概率分别为![]() 和
和![]() ,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
(1)求恰好有一种新产品研发成功的概率;
(2)若新产品A研发成功,预计企业可获得利润120万元,不成功则会亏损50万元;若新产品B研发成功,企业可获得利润100万元,不成功则会亏损40万元,求该企业获利ξ万元的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
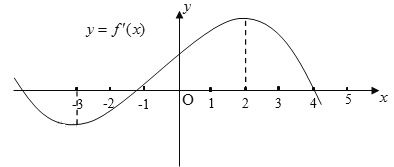
【题目】如果函数![]() 的导函数
的导函数![]() 的图象如图所示,则以下关于函数
的图象如图所示,则以下关于函数![]() 的判断:
的判断:
①在区间![]() 内单调递增;
内单调递增;
②在区间![]() 内单调递减;
内单调递减;
③在区间![]() 内单调递增;
内单调递增;
④![]() 是极小值点;
是极小值点;
⑤![]() 是极大值点.
是极大值点.
其中正确的是( )
A. ③⑤B. ②③C. ①④⑤D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3月3日,武汉大学人民医院的团队在预印本平台![]() 上发布了一项研究:在新冠肺炎病例的统计数据中,男性患者往往比女性患者多.研究者分析了1月1日~29日的6013份病例数据,发现
上发布了一项研究:在新冠肺炎病例的统计数据中,男性患者往往比女性患者多.研究者分析了1月1日~29日的6013份病例数据,发现![]() 的患者为男性;进入重症监护病房的患者中,则有
的患者为男性;进入重症监护病房的患者中,则有![]() 为男性.随后,他们分析了武汉大学人民医院的数据.他们按照症状程度的不同进行分析,结果发现,男性患者有
为男性.随后,他们分析了武汉大学人民医院的数据.他们按照症状程度的不同进行分析,结果发现,男性患者有![]() 为危重,而女性患者危重情况的为
为危重,而女性患者危重情况的为![]() .也就是说男性的发病情况似乎普遍更严重.研究者总结道:“男性在新冠肺炎的传播中扮演着重要的角色.”那么,病毒真的偏爱男性吗?有一个中学生学习小组,在自己封闭的社区进行无接触抽样问卷调查,收集到男、女患者各50个数据,统计如下:
.也就是说男性的发病情况似乎普遍更严重.研究者总结道:“男性在新冠肺炎的传播中扮演着重要的角色.”那么,病毒真的偏爱男性吗?有一个中学生学习小组,在自己封闭的社区进行无接触抽样问卷调查,收集到男、女患者各50个数据,统计如下:
轻—中度感染 | 重度(包括危重) | 总计 | |
男性患者 |
|
|
|
女性患者 |
|
|
|
总计 |
|
|
|
(1)求![]() 列联表中的数据
列联表中的数据![]() 的值;
的值;
(2)能否有![]() 把握认为,新冠肺炎的感染程度和性别有关?
把握认为,新冠肺炎的感染程度和性别有关?
(3)该学生实验小组打算从“轻—中度感染”的患者中按男女比例再抽取5人,追踪某种中药制剂的效果.然后从这5人中随机抽取3人进行每日的健康记录,求至少抽到2名女性患者的概率.
附表及公式:![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com