
���� �����⻭��ͼ�Σ�����ƽ�������ļӼ����㼰������������һ����5������ô𰸣�
��� �⣺��DΪBC�ߵ��е㣬��$\overrightarrow{PB}$+$\overrightarrow{PC}$=2$\overrightarrow{PD}$���ʢ���ȷ��
$\overrightarrow{PB}$•$\overrightarrow{PC}$=��$\overrightarrow{PD}$+$\overrightarrow{DB}$��•��$\overrightarrow{PD}$+$\overrightarrow{DC}$��=$\overrightarrow{PD}$2-$\overrightarrow{DB}$2���ʢ���ȷ��
������ɵ�$\overrightarrow{{P}_{0}B}•\overrightarrow{{P}_{0}C}$=${\overrightarrow{{P}_{0}D}}^{2}-{\overrightarrow{DB}}^{2}$������֪$\overrightarrow{PB}$•$\overrightarrow{PC}$��$\overrightarrow{{P}_{0}B}$•$\overrightarrow{{P}_{0}C}$�������
��${\overrightarrow{PD}}^{2}��{\overrightarrow{{P}_{0}D}}^{2}$����|$\overrightarrow{PD}$|��|$\overrightarrow{{P}_{0}D}$|��������ʢ۴���
ע�P0��D�Ƕ��㣬��P0D�ǵ�D��ֱ���ϸ���������Сֵ����P0D��AB����$\overrightarrow{{P}_{0}D}$•$\overrightarrow{AB}$=0��
��AB�е�ΪO����CO��P0D���ʢܴ���
����DΪBC���е㣬COΪ�ױ�AB�����ߣ���CO��AB�����ABC�ǵ��������Σ���AC=BC���ʢ���ȷ��
���Ͽ�֪���٢ڢ���ȷ��
�ʴ�Ϊ���٢ڢݣ�
���� ���⿼��ƽ�����������������㣬�������������ж���Ӧ�ã�������˼ά������������֤���������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x+y-3=0 | B�� | x+y-1=0 | C�� | x-y-3=0 | D�� | 2x-y-5=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$ | B�� | 2$\sqrt{5}$ | C�� | $\frac{3\sqrt{7}}{2}$ | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{16}$ | B�� | $-\frac{2}{5}$ | C�� | $\frac{11}{16}$ | D�� | $\frac{13}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
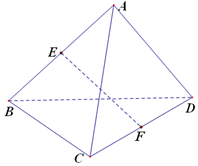 ��֪����A-BCD�ĸ����ⳤ����ȣ�E��F�ֱ�����AB��CD���е㣬��EF��BC���ɵĽ��ǣ�������
��֪����A-BCD�ĸ����ⳤ����ȣ�E��F�ֱ�����AB��CD���е㣬��EF��BC���ɵĽ��ǣ�������| A�� | 90�� | B�� | 60�� | C�� | 45�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 33 | B�� | 44 | C�� | 55 | D�� | 66 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com