
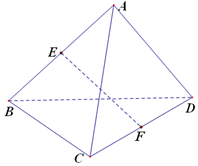
 已知三棱锥A-BCD的各个棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )
已知三棱锥A-BCD的各个棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
分析 由题意画出图形,取AC中点G,连接EG,GF,则∠GEF为EF与BC所成的角,设三棱锥A-BCD的各个棱长都是2,然后求解直角三角形得答案.
解答 解:如图,
三棱锥A-BCD的各个棱长都相等,设为2,
取AC中点G,连接EG,GF,则∠GEF为EF与BC所成的角,
且EG=GF=1,BF=$\sqrt{3}$,
正四面体A-BCD的高为$\sqrt{{2}^{2}-(\frac{2\sqrt{3}}{3})^{2}}=\frac{2\sqrt{6}}{3}$,
过E作EH⊥BF于H,则EH=$\frac{\sqrt{6}}{3}$,
∴$EF=\sqrt{(\frac{\sqrt{6}}{3})^{2}+(\frac{2\sqrt{3}}{3})^{2}}=\sqrt{2}$,
∴△EGF是以∠EGF为直角的等腰直角三角形,则∠GEF=45°.
故选:C.
点评 本题考查异面直线所成的角,考查空间想象能力和思维能力,考查计算能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2016 | C. | 4032 | D. | 4033 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | 14 | C. | 7 | D. | -14 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{13}+\frac{5}{13}i$ | B. | $-\frac{12}{13}+\frac{5}{13}i$ | C. | $-\frac{12}{13}-\frac{5}{13}i$ | D. | $\frac{12}{13}-\frac{5}{13}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com