
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
分析 (1)由表中数据,计算平均数和回归系数,写出回归直线方程即可;
(2)将x=10代入回归直线方程,计算对应$\stackrel{∧}{y}$的值即可.
解答 解:(1)由表中数据得:$\overline{x}$=$\frac{2+3+4+5}{4}$=3.5,
$\overline{y}$=$\frac{2.5+3+4+4.5}{4}$=3.5,
$\underset{\stackrel{4}{∑}}{i=1}$xiyi=52.5,
$\underset{\stackrel{4}{∑}}{i=1}$${{x}_{i}}^{2}$=54,
∴$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-x{\overline{x}}^{2}}$=0.7,
∴$\stackrel{∧}{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=1.05,
∴线性回归方程是$\stackrel{∧}{y}$=0.7x+1.05;
(2)将x=10代入回归直线方程,
得$\stackrel{∧}{y}$=0.7×10+1.05=8.05,
∴预测加工10个零件需要8.05小时.
点评 本题考查了线性回归方程的计算与应用问题,是基础题目.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆E:$\frac{x^2}{a^2}+{y^2}$=1(常数a>1),过点A(-a,0)且以t为斜率的直线与椭圆E交于点B,直线BO交椭圆E于点C(O坐标原点).
已知椭圆E:$\frac{x^2}{a^2}+{y^2}$=1(常数a>1),过点A(-a,0)且以t为斜率的直线与椭圆E交于点B,直线BO交椭圆E于点C(O坐标原点).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
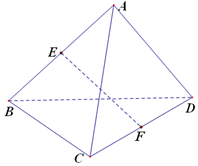 已知三棱锥A-BCD的各个棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )
已知三棱锥A-BCD的各个棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 1013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com