
分析 (1)由点An($\sqrt{{S}_{n}}$,$\sqrt{{S}_{n-1}}$)(n>1)在曲线x2-y2=n上,代入即可求得an=Sn-Sn-1=n,当n=1时,a1=1,即可求得数列{an}的通项公式;
(2)由(1)可知:cn=anbn=n•3n-1,利用“错位相减法”即可求得数列{cn}的前n项和Tn.
解答 解:(1)由点An($\sqrt{{S}_{n}}$,$\sqrt{{S}_{n-1}}$)(n>1)在曲线x2-y2=n上,
∴Sn-Sn-1=n,
则an=Sn-Sn-1=n,
当n=1时,a1=1,
∴数列{an}的通项公式an=n;
(2)由(1)可知:an=n,bn=3n-1,
则cn=anbn=n•3n-1,
数列{cn}的前n项和Tn,Tn=1•30+2•3+3•32+…+n•3n-1,①
3Tn=1•3+2•32+3•33+…+n•3n,②
①-②,得:-2Tn=1+3+32+33+…+3n-1-n•3n,
=1+$\frac{3(1-{3}^{n-1})}{1-3}$-n•3n,
=$\frac{(1-2n)•{3}^{n}}{2}$-$\frac{1}{2}$,
∴Tn=$\frac{(2n-1)•{3}^{n}}{4}$+$\frac{1}{4}$,
数列{cn}的前n项和Tn,Tn=$\frac{(2n-1)•{3}^{n}}{4}$+$\frac{1}{4}$.
点评 本题考查数列的递推公式,考查数列通项公式的求法,考查“错位相减法”求数列的前n项和,考查计算能力,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:选择题
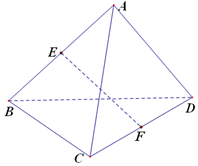 已知三棱锥A-BCD的各个棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )
已知三棱锥A-BCD的各个棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
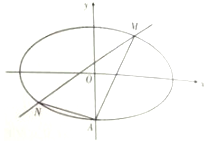 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点$(\sqrt{2},0)$,且焦距为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点$(\sqrt{2},0)$,且焦距为2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 1013 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 温差x(℃) | 10 | 11 | 13 | 12 | 8 |
| 发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com