
分析 (1)求出函数的导数,求得切线的斜率,解方程可得a;
(2)由导数大于0,可得增区间;由导数小于0,可得减区间,结合正弦函数的图象及性质.
解答 解:(1)函数f(x)=cosx+a•x的导数为f′(x)=a-sinx,
由题意可得a-sin$\frac{π}{6}$=0,解得a=$\frac{1}{2}$;
(2)由f′(x)=$\frac{1}{2}$-sinx>0,解得2kπ-$\frac{7π}{6}$<x<2kπ+$\frac{π}{6}$,k∈Z,
由f′(x)<0,解得2kπ+$\frac{π}{6}$<x<2kπ+$\frac{5π}{6}$,k∈Z,
即有单调增区间为(2kπ-$\frac{7π}{6}$,2kπ+$\frac{π}{6}$),
单调减区间为(2kπ+$\frac{π}{6}$,2kπ+$\frac{5π}{6}$),k∈Z.
点评 本题考查导数的运用:求切线的斜率和单调区间,同时考查三角函数的图象和性质,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
| 患心脏病 | 未患心脏病 | 合计 | |
| 每一晚都打鼾 | 3 | 17 | a= |
| 不打鼾 | 2 | 128 | b= |
| 合计 | c= | d= | n= |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1,-7) | B. | (5,13,-3) | C. | (-3,1,5) | D. | (5,3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n⊥β,且α⊥β,则m∥n | B. | 若α∥β,m?α,n?β,则m∥n | ||
| C. | 若m⊥α,n⊥β,m⊥n,则α⊥β | D. | 若m⊥n,m?α,n?β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
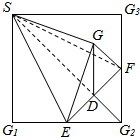 如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com