
分析 如果连接AG并延长,交BC于点P,由三角形的重心的性质可知AG=2GP,则AG:AP=2:3.又EF∥BC,根据相似三角形的判定可知△AGF∽△APC,得出AF:AC=2:3,最后由EF∥BC,得出△AEF∽△ABC,从而求出EF:BC=AF:AC=2:3,问题得以解决.
解答 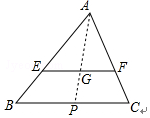 解:如图,连接AG并延长,交BC于点P.
解:如图,连接AG并延长,交BC于点P.
∵G为△ABC的重心,
∴AG=2GP,
∴AG:AP=2:3,
∵EF过点G且EF∥BC,
∴△AGF∽△APC,
∴AF:AC=AG:AP=2:3.
又∵EF∥BC,
∴△AEF∽△ABC,
∴EF:BC=AF:AC=2:3.
∵$\overrightarrow{BC}$=$\overrightarrow{a}$,
∴$\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{BC}$=$\frac{2}{3}$$\overrightarrow{a}$
故答案为:$\frac{2}{3}$$\overrightarrow{a}$
点评 此题主要考查了三角形的重心的性质,相似三角形的判定及性质,三角形三边的中线相交于一点,这点叫做三角形的重心.重心到顶点的距离等于它到对边中点距离的两倍,平行于三角形一边的直线截其它两边,所得三角形与原三角形相似,相似三角形的三边对应成比例,以及向量的知识.


科目:高中数学 来源: 题型:解答题
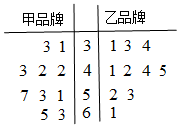 某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.
某商场对甲、乙两种品牌的商品进行为期100天的营销活动,为调查这100天的日销售情况,随机抽取了10天的日销售量(单位:件)作为样本,样本数据的茎叶图如图.若日销量不低于50件,则称当日为“畅销日”.| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
| 畅销日天数 | 非畅销日天数 | 合计 | |
| 甲品牌 | 50 | 50 | 100 |
| 乙品牌 | 30 | 70 | 100 |
| 合计 | 80 | 120 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1] | B. | (-1,1) | C. | [-1,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {0,1,2} | C. | {-1,0,1} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$-cos1 | B. | $\frac{{π}^{2}}{2}$+1 | C. | π | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com