
椭圆E: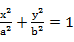 (a>b>0)的焦点到直线x-3y=0的距离为
(a>b>0)的焦点到直线x-3y=0的距离为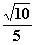 ,离心率为
,离心率为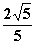 ;抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点,与E交于A,B,与G交于C,D.
;抛物线G:y2=2px(p>0)的焦点与椭圆E的焦点重合;斜率为k的直线l过G的焦点,与E交于A,B,与G交于C,D.
(1)求椭圆E及抛物线G的方程;
(2)是否存在常数λ,使 为常数,若存在,求出λ的值,若不存在,请说明理由.
为常数,若存在,求出λ的值,若不存在,请说明理由.
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
某学生对一些对数进行运算,如下图表格所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是 ( )
A.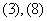 B.
B.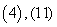 C.
C.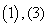 D.
D.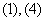
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)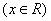 满足f(
满足f(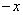 )=f(x),f(x)=f(2
)=f(x),f(x)=f(2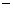 x),且当
x),且当 时,f(x)=x3.又函数g(x)=|xcos
时,f(x)=x3.又函数g(x)=|xcos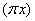 |,则函数h(x)=g(x)-f(x)在
|,则函数h(x)=g(x)-f(x)在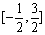 上的零点个数为
上的零点个数为
(A)5 (B)6 (C)7 (D)8
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD·BC;类似地有命题:在三棱锥A-BCD中,AD⊥平面ABC,若A点在平面BCD内的射影为M,则有S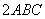 =S△BCM·S△BCD.上述命题是( )
=S△BCM·S△BCD.上述命题是( )
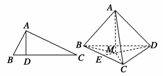
A.真命题
B.增加条件“AB⊥AC”才是真命题
C.增加条件“M为△BCD的垂心”才是真命题
D.增加条件“三棱锥A-BCD是正三棱锥”才是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com