
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{4}$ |
分析 本题是一个古典概型,试验发生包含的事件(a,b)的取值所有可能的结果可以列举出,满足条件的事件直线不经过第四象限,符合条件的(a,b)有2种结果,根据古典概型概率公式得到结果.
解答 解:由题意知本题是一个古典概型,试验发生包含的事件a∈A={-2,-1,1},b∈B={-1,1,3},
得到(a,b)的取值所有可能的结果有:
(-2,-1);(-2,1);(-2,3);(-1,-1);(-1,1);(-1,3);(2,-1);(2,1);(2,3)共9种结果.
由ax-y+b=0得y=ax+b,当$\left\{\begin{array}{l}{a>0}\\{b≥0}\end{array}\right.$时,直线不经过第四限,符合条件的(a,b)有(2,1);(2,3),2种结果,
∴直线不过第四象限的概率P=$\frac{2}{9}$,
故选:A.
点评 本题主要考查古典概型的概率的计算,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、体积的比值得到,属于基础题.


科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
一直三棱柱的每条棱长都是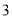 ,且每个顶点都在球
,且每个顶点都在球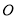 的表面上,则球
的表面上,则球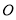 的半径为( )
的半径为( )
A.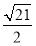 B.
B.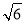 C.
C.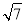 D.
D.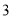
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2}]$ | B. | $[\frac{1}{2},+∞)$ | C. | $(0,6+2\sqrt{7})$ | D. | $(0,6-2\sqrt{7})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+1)2+y2=1 | B. | (x-1)2+y2=1 | C. | x2+y2=1 | D. | x2+(y-1)2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com