
| A�� | 3�� | B�� | 2�� | C�� | 1�� | D�� | 0�� |
���� �������⣬��x1f��x1��+x2f��x2����x1f��x2��+x2f��x1�����οɵ�[f��x1��-f��x2��]��x1-x2����0�����������ɵ�������f��x��Ϊ��H������������f��x��Ϊ�����������������ݴ����η������������ĵ����ԣ��ۺϿɵô𰸣�
��� �⣺�������⣬����x1f��x1��+x2f��x2����x1f��x2��+x2f��x1����
����f��x1����x1-x2��-f��x2����x1-x2����0��
��[f��x1��-f��x2��]��x1-x2����0��
�����ɵã�������f��x��Ϊ��H������������f��x��Ϊ����������������
���ڢ١�y=-x3+x+l����y��=-3x2+l������������Ҳ���dz������������䲻�ǡ�H��������
���ڢڡ�y=3x-2��sinx-cosx������y��=3-2��sinx+cosx��=3-2$\sqrt{2}$sin��x+$\frac{��}{4}$������y���0��
y=3x-2��sinx-cosx��Ϊ�������������ǡ�H��������
���ڢۡ�y=l-ex=-ex+1���Ǽ����������䲻�ǡ�H��������
���ڢܡ�f��x��=$\left\{\begin{array}{l}{lnx��x��1��}\\{0��x��1��}\end{array}\right.$����x��1ʱ�dz�����������x��1ʱ���������������ǡ�H��������
�ʡ�H��������2����
��ѡ��B��
���� ���⿼�麯�������Ե��ж���Ӧ�ã��ؼ�������x1f��x1��+x2f��x2����x1f��x2��+x2f��x1�����жϳ������ĵ����ԣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��\frac{4}{9}��\frac{8}{9}��$ | B�� | $��\frac{2}{9}��\frac{4}{9}��$ | C�� | ��2��0�� | D�� | ��9��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$i | B�� | $\frac{1}{2}$i | C�� | -$\frac{1}{2}$ | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $8\sqrt{2}��$ | B�� | $8��3-\sqrt{2}����$ | C�� | $16��\sqrt{2}-1����$ | D�� | $16��2-\sqrt{2}����$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $?x�ʣ�1��+�ޣ���x_0^2+2{x_0}+2��0$ | B�� | $?x�ʣ�{-�ޣ�1}]��x_0^2+2{x_0}+2��0$ | ||
| C�� | $?{x_0}�ʣ�1��+�ޣ���x_0^2+2{x_0}+2��0$ | D�� | $?{x_0}�ʣ�{-�ޣ�1}]��x_0^2+2{x_0}+2��0$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
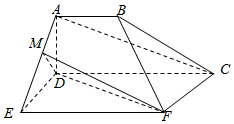 ��ͼ���ռ伸����ADE-BCF�У��ı���ABCD�����Σ��ı���CDEF
��ͼ���ռ伸����ADE-BCF�У��ı���ABCD�����Σ��ı���CDEF�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com