
���� ���� ��F1��-c��0����F2��c��0����������֪�����г������飬��⼴�ɣ�
����ֱ��lб�ʴ���ʱ����M��x1��y1����N��x2��y2����ֱ��lΪ��y=k��x-1��������$\frac{x^2}{2}+{y^2}=1$����Τ�ﶨ�����Ƴ�$\overrightarrow{{F_1}M}•\overrightarrow{{F_1}N}��[-1��\frac{7}{2}��$����ֱ��lб�ʲ�����ʱ��$\left\{\begin{array}{l}x=1\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.��y=��\frac{{\sqrt{2}}}{2}$���Ƴ�$\overrightarrow{{F_1}M}•\overrightarrow{{F_1}N}=��2��\frac{{\sqrt{2}}}{2}��•��2��-\frac{{\sqrt{2}}}{2}��=\frac{7}{2}$��
��� ����С������12�֣�
�⣺���� ��F1��-c��0����F2��c��0��
��$\left\{\begin{array}{l}\frac{c}{a}=\frac{{\sqrt{2}}}{2}\\ a-c=\sqrt{2}-1\end{array}\right.��\left\{\begin{array}{l}a=\sqrt{2}\\ c=1\end{array}\right.$-------------��2�֣�
��b2=a2-c2=1����$\frac{x^2}{2}+{y^2}=1$-------------------------------��4�֣�
����ֱ��lб�ʴ���ʱ����M��x1��y1����N��x2��y2����ֱ��lΪ��y=k��x-1��������$\frac{x^2}{2}+{y^2}=1$
�ã�$\frac{x^2}{2}+{k^2}{��x-1��^2}=1�������ã�$��1+2k2��x2-4k2x+2k2-2=0�����������0
����${x_1}+{x_2}=\frac{{4{k^2}}}{{2{k^2}+1}}��{x_1}{x_2}=\frac{{2{k^2}-2}}{{2{k^2}+1}}$��--------------------------------------��7�֣�
����$\overrightarrow{{F_1}M}•\overrightarrow{{F_1}N}=��{x_1}+1��{y_1}��•��{x_2}+1��{y_2}��={x_1}{x_2}+{x_1}+{x_2}+1+{k^2}��{x_1}-1����{x_2}-1��$=$��1+{k^2}��{x_1}{x_2}+��1-{k^2}����{x_1}+{x_2}��+1+{k^2}=��1+{k^2}��\frac{{2{k^2}-2}}{{2{k^2}+1}}+��1-{k^2}��\frac{{4{k^2}}}{{2{k^2}+1}}+1+{k^2}$=$\frac{{7{k^2}-1}}{{2{k^2}+1}}=\frac{{\frac{7}{2}��2{k^2}+1��-\frac{9}{2}}}{{2{k^2}+1}}=\frac{7}{2}-\frac{{\frac{9}{2}}}{{2{k^2}+1}}$------------------------------��9�֣�
��Ϊ1+2k2��1������$\overrightarrow{{F_1}M}•\overrightarrow{{F_1}N}��[-1��\frac{7}{2}��$-------------------------------��10�֣�
��ֱ��lб�ʲ�����ʱ��$\left\{\begin{array}{l}x=1\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.��y=��\frac{{\sqrt{2}}}{2}$����$M��1��\frac{{\sqrt{2}}}{2}����N��1��-\frac{{\sqrt{2}}}{2}��$
����$\overrightarrow{{F_1}M}•\overrightarrow{{F_1}N}=��2��\frac{{\sqrt{2}}}{2}��•��2��-\frac{{\sqrt{2}}}{2}��=\frac{7}{2}$--------------------��11�֣�
���ϣ�$\overrightarrow{{F_1}M}•\overrightarrow{{F_1}N}��[-1��\frac{7}{2}]$----------------------------------------��12�֣�
���� ���⿼����Բ���̵���ֱ������Բ��λ�ù�ϵ���ۺ�Ӧ�ã�����ת��˼���Լ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��e�� | B�� | ��e��10] | C�� | ��1��10] | D�� | ��10��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [0��3] | B�� | ��0��3�� | C�� | ��-�ޣ�0���ȣ�3��+�ޣ� | D�� | ��-�ޣ�0]��[3��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 0 | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
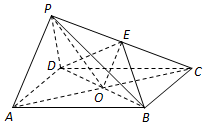 ��ͼ��������P-ABCD�У��ı���ABCDΪƽ���ı��Σ�AC��BD�ཻ�ڵ�O����EΪPC���е㣬OP=OC��PA��PD����֤��
��ͼ��������P-ABCD�У��ı���ABCDΪƽ���ı��Σ�AC��BD�ཻ�ڵ�O����EΪPC���е㣬OP=OC��PA��PD����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 2�� | C�� | 1�� | D�� | 0�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com