
| A. | 0 | B. | $\frac{24}{25}$ | C. | $\frac{16}{25}$ | D. | $\frac{24}{25}$或$\frac{16}{25}$ |
分析 由已知分别求出cosα、sin(α+β)的值,然后利用“拆角配角”的方法分类求出sinβ,则答案可求.
解答 解:∵0<α<$\frac{π}{2}$,sinα=$\frac{3}{5}$,
∴cosα=$\sqrt{1-si{n}^{2}α}=\sqrt{1-(\frac{3}{5})^{2}}=\frac{4}{5}$.
∵0<α<$\frac{π}{2}$<β<π,∴$\frac{π}{2}$<α+β<$\frac{3π}{2}$.
又cos(α+β)=-$\frac{4}{5}$,
∴sin(α+β)=$±\sqrt{1-co{s}^{2}(α+β)}=±\frac{3}{5}$.
若sin(α+β)=$\frac{3}{5}$,则sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=$\frac{3}{5}×\frac{4}{5}-(-\frac{4}{5})×\frac{3}{5}=\frac{24}{25}$;
若sin(α+β)=-$\frac{3}{5}$,则sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=$(-\frac{3}{5})×\frac{4}{5}-(-\frac{4}{5})×\frac{3}{5}$=0(舍).
∴sinβ=$\frac{24}{25}$.
故选:B.
点评 本题考查两角和与差的正弦,体现了分类讨论的数学思想方法,关键是“拆角配角”思想的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
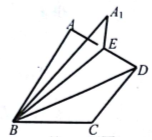 如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )
如图,在直二面角A-BD-C中,△ABD、△CBD均是以BD为斜边的等腰直角三角形,取AD中点E,将△ABE沿BE翻折到△A1BE,在△ABE的翻折过程中,下列不可能成立的是( )| A. | BC与平面A1BE内某直线平行 | B. | CD∥平面A1BE | ||
| C. | BC与平面A1BE内某直线垂直 | D. | BC⊥A1B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
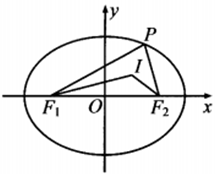 设P为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的动点,F1、F2为椭圆C的焦点,I为△PF1F2的内心,则直线IF1和直线IF2的斜率之积( )
设P为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的动点,F1、F2为椭圆C的焦点,I为△PF1F2的内心,则直线IF1和直线IF2的斜率之积( )| A. | 是定值 | B. | 非定值,但存在最大值 | ||
| C. | 非定值,但存在最小值 | D. | 非定值,且不存在最值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com