
【题目】为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.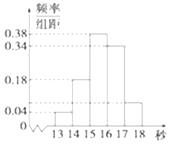
(1)设m,n表示样本中两个学生的百米测试成绩,已知m,n∈[13,14)∪[17,18],求事件“|m-n|>2”的概率;
(2)根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如附表:
根据上表数据,能否在犯错误的概率不超过0.01的前提下认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附: 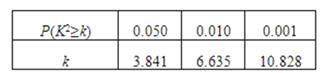
【答案】
(1)
解:从频率分布直方图中可以看出,成绩在 的人数为 (人),设为 ;成绩在 的人数为 (人),设为 .
![]() 有 一种情况;
有 一种情况; ![]() 时有 三种情况; 分别在 和 时有 六种情况,所有基本事件总数为10.
时有 三种情况; 分别在 和 时有 六种情况,所有基本事件总数为10.
而事件“ ”由6个基本事件即 组成.
所以 .
(2)
解:依题意得到相应的 列联表如下:
.
由于 ![]() ,故在犯错误的概率不超过 的前提下认为“体育达标与性别有关”.
,故在犯错误的概率不超过 的前提下认为“体育达标与性别有关”.
故可以根据男女生性别划分达标的标准.
【解析】:本题主要考查了独立性检验的应用,解决问题的关键是(1) 根据频率从分布直方图及公式 ![]() 分别求出第一组和第五组的人数.然后用例举法将从这两组中随机抽取两人的所有基本事件一一例举,然后再将
分别求出第一组和第五组的人数.然后用例举法将从这两组中随机抽取两人的所有基本事件一一例举,然后再将 ![]() 的所有事件一一例举,根据古典概型概率公式求其概率. (2)根据频率分布直方图求出不达标的总人数,则可得
的所有事件一一例举,根据古典概型概率公式求其概率. (2)根据频率分布直方图求出不达标的总人数,则可得 ![]() ,从而可得
,从而可得 ![]() 的值.根据公式计算
的值.根据公式计算 ![]() ,若
,若 ![]() 说明两变量有关,否则无关.
说明两变量有关,否则无关.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() 且经过点
且经过点![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系,设曲线
取相同的长度单位,建立极坐标系,设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 两城相距
两城相距![]() ,在两城之间距
,在两城之间距![]() 城
城![]() 处建一核电站给
处建一核电站给![]() 两城供电,为保证城市安全,核电站距城市距离不得小于
两城供电,为保证城市安全,核电站距城市距离不得小于![]() .已知供电费用等于供电距离
.已知供电费用等于供电距离![]() 的平方与供电量(亿度)之积的
的平方与供电量(亿度)之积的![]() 倍,若
倍,若![]() 城供电量为每月20亿度,城供电量为每月10亿度.
城供电量为每月20亿度,城供电量为每月10亿度.
(1)把月供电总费用![]() 表示成
表示成![]() 的函数;
的函数;
(2)核电站建在距![]() 城多远,才能使供电总费用
城多远,才能使供电总费用![]() 最少?
最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文科学生总成绩不好与数学成绩不好有关系吗?
总成绩好 | 总成绩不好 | 总计 | |
数学成绩好 | 20 | 10 | 30 |
数学成绩不好 | 5 | 15 | 20 |
总计 | 25 | 25 | 50 |
(P(K2≥3.841)≈0.05,P(K2≥6.635)≈0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司研发出一款新产品,批量生产前先同时在甲、乙两城市销售30天进行市场调查.调查结果发现:甲城市的日销售量![]() 与天数
与天数![]() 的对应关系服从图①所示的函数关系;乙城市的日销售量
的对应关系服从图①所示的函数关系;乙城市的日销售量![]() 与天数
与天数![]() 的对应关系服从图②所示的函数关系;每件产品的销售利润
的对应关系服从图②所示的函数关系;每件产品的销售利润![]() 与天数
与天数![]() 的对应关系服从图③所示的函数关系,图①是抛物线的一部分.
的对应关系服从图③所示的函数关系,图①是抛物线的一部分.
图① ,图②
,图② ,图③
,图③
(1)设该产品的销售时间为![]() ,日销售利润为
,日销售利润为![]() ,求
,求![]() 的解析式;
的解析式;
(2)若在30天的销售中,日销售利润至少有一天超过2万元,则可以投入批量生产,该产品是否可以投入批量生产,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2(a+2)x+a2 , g(x)=﹣x2+2(a﹣2)x﹣a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)},(其中max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A﹣B=( )
A.a2﹣2a﹣16
B.a2+2a﹣16
C.﹣16
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海上某货轮在A处看灯塔B在货轮的北偏东75°,距离为12![]() 海里;在A处看灯塔C在货轮的北偏西30°,距离为8
海里;在A处看灯塔C在货轮的北偏西30°,距离为8![]() 海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
海里;货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°.(要画图)
(1)A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】轴截面是边长为4 ![]() 的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为
的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为 ![]() ,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )
,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( ) 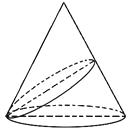
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com