
【题目】轴截面是边长为4 ![]() 的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为
的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为 ![]() ,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )
,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( ) 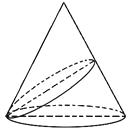
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解答:本题综合考查空间几何体中的线面关系与解析几何中直线与直线的位置关系以及平面几何中圆的相关定理的应用,意在考查数形结合思想与空间想象能力. 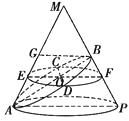
如图,根据轴截面是边长为4 ![]() 的等边三角形,可知椭圆的长轴长为AB=6,设O为椭圆的中心,则a=OB=OA=3,过O作平行于底面的平面,可得到截面圆,交椭圆于两点C、D,则C、D即是椭圆短半轴的顶点.根据题意知AB⊥BF,在直角三角形OBF中,∠OBF=90°,所以FO=2
的等边三角形,可知椭圆的长轴长为AB=6,设O为椭圆的中心,则a=OB=OA=3,过O作平行于底面的平面,可得到截面圆,交椭圆于两点C、D,则C、D即是椭圆短半轴的顶点.根据题意知AB⊥BF,在直角三角形OBF中,∠OBF=90°,所以FO=2 ![]() ,F是BP的中点,过点B作AP的平行线,交AM于点G,则E是AG的中点,所以OE=
,F是BP的中点,过点B作AP的平行线,交AM于点G,则E是AG的中点,所以OE= ![]() AP=
AP= ![]() ,由相交弦定理得CO2=OF×OE,所以b2=6,所以c2=a2-b2=3,所以椭圆的离心率为
,由相交弦定理得CO2=OF×OE,所以b2=6,所以c2=a2-b2=3,所以椭圆的离心率为 ![]() .
.
分析:本题主要考查了平面与圆锥面的截线,解决问题的关键是根据平面与圆锥面的截线满足的有关条件通过构造辅助线结合所学椭圆性质及相交弦定理计算即可


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.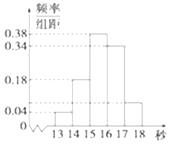
(1)设m,n表示样本中两个学生的百米测试成绩,已知m,n∈[13,14)∪[17,18],求事件“|m-n|>2”的概率;
(2)根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如附表:
根据上表数据,能否在犯错误的概率不超过0.01的前提下认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附: 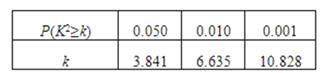
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
参考公式及数据: 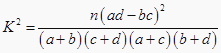
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B. 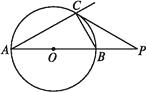
(1)试探索∠BCP与∠P的数量关系;
(2)若∠A=30°,则PB与PA有什么关系?
(3)∠A可能等于45°吗?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1<x<3},集合B={x|2m<x<1-m}.
(1)当m=-1时,求A∪B;
(2)若AB,求实数m的取值范围;
(3)若A∩B=,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com