
如图4,空间四边形ABCD中,若AD=4,BC=4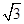 ,E、F分别为AB、CD中点,且EF=4,则AD与BC所成的角是 .
,E、F分别为AB、CD中点,且EF=4,则AD与BC所成的角是 . 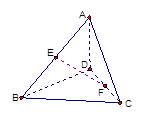
科目:高中数学 来源: 题型:填空题
多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点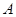 在平面
在平面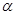 内,其余顶点在
内,其余顶点在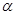 的同侧,正方体上与顶点
的同侧,正方体上与顶点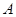 相邻的三个顶点到
相邻的三个顶点到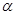 的距离分别为1,2和4,
的距离分别为1,2和4,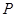 是正方体的其余四个顶点中的一个,则
是正方体的其余四个顶点中的一个,则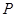 到平面
到平面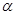 的距离可能是:
的距离可能是:
①3; ②4; ③5; ④6; ⑤7
以上结论正确的为______________。(写出所有正确结论的编号)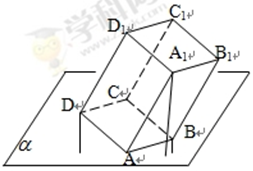
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
将正方形ABCD沿对角线BD折成直二面角 ,有如下四个结论:
,有如下四个结论:
①AC⊥BD;② 是等边三角形;③
是等边三角形;③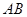 与
与 所成的角为
所成的角为 ;④
;④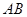 与平面
与平面 成
成 的角。
的角。
其中正确的结论的序号是 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列命题:
①如果 ,
, 是两条直线,且
是两条直线,且 //
// ,那么
,那么 平行于经过
平行于经过 的任何平面;
的任何平面;
②如果平面 不垂直于平面
不垂直于平面 ,那么平面
,那么平面 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面 ;
;
③若直线 ,
, 是异面直线,直线
是异面直线,直线 ,
, 是异面直线,则直线
是异面直线,则直线 ,
, 也是异面直线;
也是异面直线;
④已知平面 ⊥平面
⊥平面 ,且
,且 ∩
∩ =
= ,若
,若 ⊥
⊥ ,则
,则 ⊥平面
⊥平面 ;
;
⑤已知直线 ⊥平面
⊥平面 ,直线
,直线 在平面
在平面 内,
内, //
// ,则
,则 ⊥
⊥ .
.
其中正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com