
 设a∈R,f(x)=cosx(asinx-cosx)+cos2$({\frac{π}{2}-x})$满足f $({-\frac{π}{3}})$=f(0),
设a∈R,f(x)=cosx(asinx-cosx)+cos2$({\frac{π}{2}-x})$满足f $({-\frac{π}{3}})$=f(0),分析 (1)利用对函数解析式化简整理,进而根据三角函数的性质求得函数的解析式.
(2)直接作图即可,
(2)根据x的范围,最后根据三角函数图象和性质求得函数的最大和最小值
解答 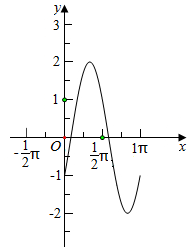 解:(1)f(x)=cosx(asinx-cosx)+cos2$({\frac{π}{2}-x})$=acosxsinx-cos2x+sin2x=$\frac{a}{2}$sin2x-cos2x,
解:(1)f(x)=cosx(asinx-cosx)+cos2$({\frac{π}{2}-x})$=acosxsinx-cos2x+sin2x=$\frac{a}{2}$sin2x-cos2x,
由f $({-\frac{π}{3}})$=f(0)得-$\frac{\sqrt{3}}{2}$•$\frac{a}{2}$+$\frac{1}{2}$=-1,解得a=2$\sqrt{3}$,
因此f(x)=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$),
(2)图象如图所示:
(3)当x∈[$\frac{π}{4}$,$\frac{π}{3}$]时,f(x)为增函数,当x∈[$\frac{π}{3}$,$\frac{11π}{24}$]时,f(x)为减函数,
所以函数f(x)在[$\frac{π}{4}$,$\frac{11π}{24}$]上的最大值为f($\frac{π}{3}$)=2,
又因为f($\frac{π}{4}$)=$\sqrt{3}$,f($\frac{11π}{24}$)=$\sqrt{2}$,
故f(x)的最小值为$\sqrt{2}$.
点评 本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.考查了学生对三角函数基础知识的灵活运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,f(x0)≥g(x0)≥h(x0) | B. | ?x0∈R,f(x0)≥g(x0)或g(x0)≥h(x0) | ||
| C. | ?x∈R,f(x)≥g(x)≥h(x) | D. | ?x∈R,f(x)≥g(x)或g(x)≥h(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为${P_0}(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )
为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针指向位置P(x,y),若初如位置为${P_0}(\frac{{\sqrt{3}}}{2},\frac{1}{2})$,秒针从P0(注:此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t的函数关系为( )| A. | $y=sin(\frac{π}{30}t+\frac{π}{6})$ | B. | $y=sin(-\frac{π}{60}t-\frac{π}{6})$ | C. | $y=sin(-\frac{π}{30}t+\frac{π}{6})$ | D. | $y=sin(-\frac{π}{30}t-\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
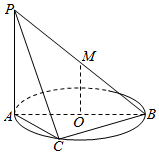 如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:
如图,直线PA垂直于圆O所在的平面,△ABC内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{2}{5}$,$\frac{9}{5}$) | B. | (-$\frac{2}{5}$,$\frac{9}{5}$) | C. | ($\frac{2}{5}$,-$\frac{9}{5}$) | D. | (-$\frac{2}{5}$,-$\frac{9}{5}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com