
分析 (1)求出数列的首项和公比,即可求数列{an}的通项公式;
(2)①求出数列的前几项,根据等差数列的性质建立方程即可求出t,②讨论m的取值,根据Tm=2cm+1的关系进行求解即可.
解答 解:(1)当n=1时,a1=S1=21+1-2=4-2=2,
a2=S2=-S1=22+1-2-2=8-4=4,
则公比q=$\frac{{a}_{2}}{{a}_{1}}$=$\frac{4}{2}$=2,
则an=2•2n-1=2n,…4分
(2)①当n=1时,得b1=6-t,n=2时,得b2=6-$\frac{1}{2}$t;n=3时,b3=$\frac{54-3t}{7}$,
则由b1+b3=2b2,得t=4.而当t=4时,由6n2-(t+3bn)n+2bn=0 得bn=2n.
由bn+1-bn=2,得 数列{bn}为等差数列,满足条件.
②由题意知,c1=a1=2,c2=c3=2,c4=a2=4,c5=c6=c7=c8=2,c9=a3=8,
则当m=1时,T1=2≠2c2,不合题意,舍去;
当m=2时,T2=c1+c2=4=2c3,满足题意,则m=2成立;
当m≥3 时,若cm+1=2,则Tm≠2cm+1,不合题意,舍去;从而cm+1 必是数列{an}中的某一项ak+1,
则Tm=a1+$\underset{\underbrace{2+…+2}}{{b}_{1}}$+a2+$\underset{\underbrace{2+…+2}}{{b}_{2}个}$+a3+$\underset{\underbrace{2+…+2}}{{b}_{3}个}$+a4+…+ak+$\underset{\underbrace{2+…+2}}{{b}_{k}个}$
=(2+22+23+…+2k)+2(b1+b2+…+bk)=2(2k-1)+2×$\frac{(2+2k)k}{2}$=2k+1+2k2+2k-2,
又2cm+1=2ak+1=2×2k+1,
所以2k+1+2k2+2k-2=2×2k+1,
即2k-k2-k+1=0,所以 2k+1=k2+k=k(k+1)
因为2k+1为奇数,而k(k+1)为偶数,所以上式无解.
即当m≥3时,Tm≠2cm+1,综上所述,满足题意的正整数仅有m=2.…16分
点评 本题主要考查等比数列和等差数列的综合应用,考查学生的运算和推理能力,综合性较强,有一定的难度.


科目:高中数学 来源: 题型:解答题
 如图,一个直角走廊的宽分别为a米、b米,一铁棒欲通过该直角走廊,设铁棒与廊壁成θ角.求:
如图,一个直角走廊的宽分别为a米、b米,一铁棒欲通过该直角走廊,设铁棒与廊壁成θ角.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
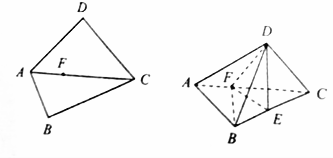 如图,平面四边形ABCD中,∠B=∠D=90°,AC=2AB=4$\sqrt{3}$,DA=DC,F是AC上一点,且AF=$\frac{1}{3}$AC.将该四边形沿AC折起,使点D在平面ABC的射影E恰在BC上,此时DE=2$\sqrt{2}$.
如图,平面四边形ABCD中,∠B=∠D=90°,AC=2AB=4$\sqrt{3}$,DA=DC,F是AC上一点,且AF=$\frac{1}{3}$AC.将该四边形沿AC折起,使点D在平面ABC的射影E恰在BC上,此时DE=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com