
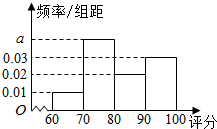
 为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.
为检测某种零件的生产质量,检验人员需抽取同批次的零件样本进行检测指标评分.若检测后评分结果大于60分的零件为合格零件,评分结果不超过40分的零件将直接被淘汰,评分结果在(40,60]内的零件可能被修复也可能被淘汰.现检验员小张检测出200个合格零件,根据指标评分绘制的频率分布直方图如图所示.| 零件评分结果所在区间 | (40,50] | (50,60] |
| 每个零件个数被修复的概率 | $\frac{1}{3}$ | $\frac{1}{2}$ |
分析 (1)由频率分布直方图中小矩形面积之和为1,能求出a.
(2)由频率分布直方图,能估计这200个零件评分结果的平均数和中位数.
(2)①由题意得评分结果在(40,50],(50,60]内零件各2个,记这5个零件被修复的个数为随机变量X,则这5个零件中,至多有2个不被修复而淘汰的概率:p=P(X=3)+P(X=4),由此能求出结果.
②由题意X的可能取值为0,1,2,3,4,分别求出相应的概率,由此能求出X的分布列和数学期望.
解答 解:(1)由频率分布直方图,得:
10(0.01+0.02+0.03+a)=1,
解得a=0.04.
(2)由频率分布直方图,估计这200个零件评分结果的平均数:
$\overline{x}$=10(65×0.01+75×0.04+85×0.02+95×0.03)=82.
由频率分布直方图,知前2个矩形面积之和为0.5,∴中位数为80.
(2)①由题意得评分结果在(40,50],(50,60]内零件各2个,
记这5个零件被修复的个数为随机变量X,
则这5个零件中,至多有2个不被修复而淘汰的概率:p=P(X=3)+P(X=4),
∵P(X=3)=$\frac{1}{2}×\frac{1}{2}×{C}_{2}^{1}×\frac{1}{3}×\frac{2}{3}+{C}_{2}^{1}×\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{1}{3}$=$\frac{1}{6}$,
P(X=4)=$\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{1}{3}$=$\frac{1}{36}$,
∴这5个零件中,至多有2个不被修复而淘汰的概率:p=P(X=3)+P(X=4)=$\frac{7}{36}$.
②由题意X的可能取值为0,1,2,3,4,
P(X=0)=$\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{2}{3}$=$\frac{1}{9}$,
P(X=1)=${C}_{2}^{1}×\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{2}{3}+\frac{1}{2}×\frac{1}{2}×{C}_{2}^{1}×\frac{1}{3}×\frac{2}{3}$=$\frac{1}{3}$,
P(X=2)=$\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{1}{3}$+$\frac{1}{2}×\frac{1}{2}×\frac{2}{3}×\frac{2}{3}$+${C}_{2}^{1}×\frac{1}{2}×\frac{1}{2}×{C}_{2}^{1}×\frac{1}{3}×\frac{2}{3}$=$\frac{13}{36}$,
P(X=3)=$\frac{1}{2}×\frac{1}{2}×{C}_{2}^{1}×\frac{1}{3}×\frac{2}{3}+{C}_{2}^{1}×\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{1}{3}$=$\frac{1}{6}$,
P(X=4)=$\frac{1}{2}×\frac{1}{2}×\frac{1}{3}×\frac{1}{3}$=$\frac{1}{36}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{9}$ | $\frac{1}{3}$ | $\frac{13}{36}$ | $\frac{1}{6}$ | $\frac{1}{36}$ |
点评 本题考查频率公布直方图的应用,考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
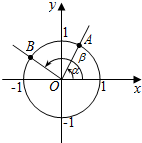 在平面直角坐标系xOy中,角$α,β(0<α<\frac{π}{2}<β<π)$的顶点与原点O重合,始边与x轴的正半轴重合,终边分别与单位圆交于A,B两点,A,B两点的横坐标分别为$\frac{5}{13},-\frac{4}{5}$.
在平面直角坐标系xOy中,角$α,β(0<α<\frac{π}{2}<β<π)$的顶点与原点O重合,始边与x轴的正半轴重合,终边分别与单位圆交于A,B两点,A,B两点的横坐标分别为$\frac{5}{13},-\frac{4}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M、N,设BM=x,x∈(0,1),给出以下四个命题:| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com