
���� ����ͶӰ����г����̽�������нǣ����������������ģ����ʽ���㣮
��� �⣺��$\overrightarrow{a}��\overrightarrow{b}$�н�Ϊ�ȣ���cos��=3cos�ȣ���cos��=0��$��=\frac{��}{2}$��
��$\overrightarrow{a}•\overrightarrow{b}$=0���ࣨ$\overrightarrow{a}-\overrightarrow{b}$��2=${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}-2\overrightarrow{a}•\overrightarrow{b}$=10����|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{10}$��
�ʴ�Ϊ$\sqrt{10}$��
���� ���⿼����ƽ�����������������㼰ģ�����㣬���ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��a��b | B�� | 0��b��a��1 | C�� | a=b | D�� | 1��b��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
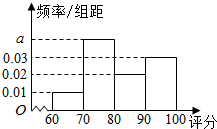 Ϊ���ij�����������������������Ա���ȡͬ���ε�����������м��ָ�����֣����������ֽ������60�ֵ����Ϊ�ϸ���������ֽ��������40�ֵ������ֱ�ӱ���̭�����ֽ���ڣ�40��60]�ڵ�������ܱ���Ҳ���ܱ���̭���ּ���ԱС�ż���200���ϸ����������ָ�����ֻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
Ϊ���ij�����������������������Ա���ȡͬ���ε�����������м��ָ�����֣����������ֽ������60�ֵ����Ϊ�ϸ���������ֽ��������40�ֵ������ֱ�ӱ���̭�����ֽ���ڣ�40��60]�ڵ�������ܱ���Ҳ���ܱ���̭���ּ���ԱС�ż���200���ϸ����������ָ�����ֻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��| ������ֽ���������� | ��40��50] | ��50��60] |
| ÿ��������������ĸ��� | $\frac{1}{3}$ | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{3}$ | B�� | $\frac{2}{3}$ | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{5}+1}{2}$ | B�� | $\frac{\sqrt{3}}{2}$+1 | C�� | $\frac{\sqrt{3}+1}{2}$ | D�� | $\frac{\sqrt{2}+1}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com