
已知函数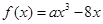 与
与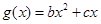 的图像都过点
的图像都过点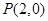 ,且它们在点
,且它们在点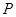 处有公共切线.
处有公共切线.
(1)求函数 和
和 的表达式及在点
的表达式及在点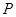 处的公切线方程;
处的公切线方程;
(2)设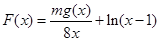 ,其中
,其中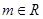 ,求
,求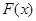 的单调区间.
的单调区间.
(1) ,
, ,
, ;
;
(2)当 时,F(x)的单调减区间是
时,F(x)的单调减区间是 单调增区间是
单调增区间是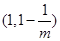 ;
;
当 时,F(x)没有单调减区间,单调增区间是
时,F(x)没有单调减区间,单调增区间是 .
.
解析试题分析:(1)因为函数 和
和 有公共的切线,所以切线的斜率相同,又因为它们都过
有公共的切线,所以切线的斜率相同,又因为它们都过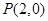 ,所以可以列出方程,求出
,所以可以列出方程,求出 ;(2)先求导数,求出函数的定义域,通过讨论
;(2)先求导数,求出函数的定义域,通过讨论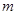 的正负,求导求单调区间.
的正负,求导求单调区间.
试题解析:(1)∵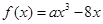 过点
过点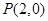
∴ ,
, , (2分)
, (2分)
∵ ,∴切线的斜率
,∴切线的斜率 .
.
∵ ,
, (1)
(1)
又∵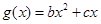 的图像过点
的图像过点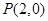 ∴
∴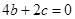 (2)
(2)
联立(1)(2)解得: (4分)
(4分)
∴ ;切线方程为
;切线方程为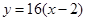 ,即
,即
∴ ,
, ;切线为:
;切线为: (6分)
(6分)
(2)∵ ,
,
∴ (9分)
(9分)
①当 时,
时,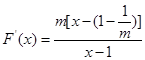 , ∵
, ∵ ,∴
,∴
又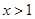 ,∴当
,∴当 时,
时, ;
;
当 时,
时, .
.
∴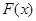 的单调减区间是
的单调减区间是 单调增区间是
单调增区间是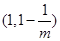 ; (11分)
; (11分)
②当 时,显然
时,显然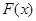 没有单调减区间,单调增区间是
没有单调减区间,单调增区间是 . (13分)
. (13分)
考点:1.利用导数求切线方程;2.利用导数求单调区间.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)= +aln(x-1)(a∈R).
+aln(x-1)(a∈R).
(Ⅰ)若f(x)在[2,+∞)上是增函数,求实数a的取值范围;
(Ⅱ)当a=2时,求证:1- <2ln(x-1)<2x-4(x>2);
<2ln(x-1)<2x-4(x>2);
(Ⅲ)求证: +
+ +…+
+…+ <lnn<1+
<lnn<1+ + +
+ + (n∈N*,且n≥2).
(n∈N*,且n≥2).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设 , 已知函数
, 已知函数
(Ⅰ) 证明 在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
在区间(-1,1)内单调递减, 在区间(1, + ∞)内单调递增;
(Ⅱ) 设曲线 在点
在点 处的切线相互平行, 且
处的切线相互平行, 且 证明
证明 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com