
分析 由题意求得数列{bn}的前n通项公式及{bn}的前n项和Tn,则k≥$\frac{2n-7}{{2}^{n}}$对任意n∈N*恒成立,根据数列的单调性即可求得k的最大值,即可求得k的取值范围.
解答 解:对任意n∈N*,都有bn+1=$\frac{1}{2}$bn+$\frac{1}{4}$,则bn+1-$\frac{1}{2}$=$\frac{1}{2}$(bn+1-$\frac{1}{2}$),
则{bn-$\frac{1}{2}$}成等比数列,首项为b1-$\frac{1}{2}$=3,公比为$\frac{1}{2}$,
∴bn-$\frac{1}{2}$=3×($\frac{1}{2}$)n-1,bn=3×($\frac{1}{2}$)n-1+$\frac{1}{2}$,
∴Tn=3(1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$)+$\frac{n}{2}$=$\frac{3(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$+$\frac{n}{2}$=6(1-$\frac{1}{{2}^{n}}$)+$\frac{n}{2}$,
由式$\frac{12k}{{12+n-2{T_n}}}$≥2n-7恒成立,
化简得k≥$\frac{2n-7}{{2}^{n}}$对任意n∈N*恒成立
设cn=$\frac{2n-7}{{2}^{n}}$,则cn+1-cn=$\frac{2(n+1)-7}{{2}^{n+1}}$-$\frac{2n-7}{{2}^{n}}$=$\frac{9-2n}{{2}^{n+1}}$,
当n≥5,cn+1-cn≤0,cn+1≤cn,{cn}为单调递减数列,
当1≤n<5,cn+1-cn>0,cn+1>cn≤0,{cn}为单调递增数列
$\frac{1}{16}$=c4<c5=$\frac{3}{32}$,所以,n=5时,cn取得最大值$\frac{3}{32}$,
∴要使k≥$\frac{2n-7}{{2}^{n}}$对任意n∈N*恒成立,k≥$\frac{3}{32}$,
实数k的取值范围为[$\frac{3}{32}$,+∞),
故答案为:[$\frac{3}{32}$,+∞).
点评 本题考查数列的递推公式,等比数列的通项公式及前n项和公式,数列与函数单调性的关系,函数恒成立问题,考查计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
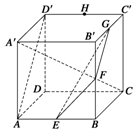 在正方体ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中点分别是E,F,G,H,如图所示.
在正方体ABCD-A′B′C′D′中,棱AB,BB′,B′C′,C′D′的中点分别是E,F,G,H,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com