
| A. | $\frac{5}{13}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{7}{24}$ |
分析 通过设乙的速度为x(m/s),则甲的速度为$\frac{11}{9}$x(m/s),利用两人达到的时间相等列出表达式、计算可知AC=1260m,进而利用余弦定理及平方关系计算即得结论.
解答 解:依题意,设乙的速度为x(m/s),则甲的速度为$\frac{11}{9}$x(m/s),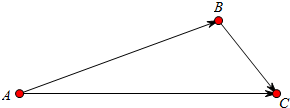
∵AB=1040m,BC=500m,
∴$\frac{AC}{x}$=$\frac{1040+500}{\frac{11}{9}x}$,
解得:AC=1260m,
∴△ABC为锐角三角形,
由余弦定理可知cos∠BAC=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{104{0}^{2}+126{0}^{2}-50{0}^{2}}{2×1040×1260}$=$\frac{84}{91}$,
∴sin∠BAC=$\sqrt{1-co{s}^{2}∠BAC}$=$\sqrt{1-(\frac{84}{91})^{2}}$=$\frac{35}{91}$=$\frac{5}{13}$,
故选:A.
点评 本题考查函数模型的选择与应用,涉及余弦定理、平方关系等基础知识,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1} | C. | [-2,0] | D. | {-2,-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
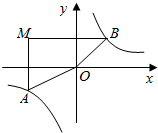 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com