
(1)求证:平面PAB⊥α;
(2)设PA中点为M,P在α上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.
剖析:(1)由于PA=PB=PC,我们寻找与平面α垂直的直线;(2)利用面面平行的判定定理,证平面OMN中有两条相交直线平行于平面PBC.
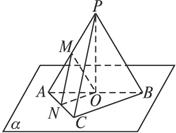
又由PA=PB=PC可知,线段PA、PB、PC在平面α上的射影长也相等,因此,P在α上的射影应是△ABC的外心,即斜边AB的中点O,连结PO,则PO⊥α,而PO平面PAB,∴平面PAB⊥α.
(2)∵PA=PB,PO⊥AB,∴AO=OB.
又ON⊥AC,BC⊥AC,
∴ON∥BC.∴ON∥平面PBC.
又OM为△PAB的中位线,
∴OM∥PB.∴OM∥平面PBC.
而OM、ON是平面OMN内两条相交直线,
∴平面OMN∥平面PBC.
讲评:要熟练掌握射影与三角形心的关系:设平面ABC外一点P在其上的射影为O,若P到三顶点距离相等,则O是外心;若P到三边距离相等,则O是内心;若两组对棱分别垂直,则O是垂心.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源:2013届内蒙古呼伦贝尔市高二上学期第一次综合考试理科数学 题型:解答题
(本题满分8分)如图,已知△ABC在平面α外,它的三边所在直线分别交平面α于点P、Q、R,求证:P、Q、R三点共线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com